LeetCode 153. Find Minimum in Rotated Sorted Array

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

LeetCode 153. Find Minimum in Rotated Sorted Array 原题链接中等

作者：

yxc , 2018-05-31 22:38:08 , 所有人可见 , 阅读 3845

18

8

题目描述

现有一个有序数组，假设从某个数开始将它后面的数按顺序放到了数组前面。
(即 [0,1,2,4,5,6,7] 可能变成 [4,5,6,7,0,1,2])。

请找出数组中的最小元素。

数组中不包含重复元素。

样例1

输入：[3,4,5,1,2] 
输出：1

样例2

输入：[4,5,6,7,0,1,2]
输出：0

算法

(二分) $O(logn)$

处理这种问题有个常用技巧：如果不想处理边界情况，比如当数组只有两三个数的时候，代码会出问题。我们可以在数组长度太短(这道题中我们判断数组长度小于5)时，直接暴力循环做；数组有一定长度时再用二分做。
这样做并不会影响算法的时间复杂度，但会缩短写代码的时间。

为了便于理解，我们将数组中的数画在二维坐标系中，横坐标表示数组下标，纵坐标表示数值，如下所示：
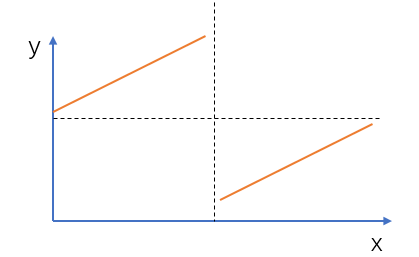
QQ图片20180531223152.png

我们会发现数组中最小值前面的数 $nums[i]$ 都满足：$nums[i] \ge nums[0]$，其中 $nums[n-1]$ 是数组最后一个元素；而数组中最小值后面的数（包括最小值）都不满足这个条件。
所以我们可以二分出最小值的位置。

另外，不要忘记处理数组完全单调的特殊情况。

时间复杂度分析：二分查找，所以时间复杂度是 $O(logn)$。

C++ 代码

class Solution {
public:
    int findMin(vector<int>& nums) {
        if (nums.back() > nums[0]) return nums[0];
        int l = 0, r = nums.size() - 1;
        while (l < r)
        {
            int mid = l + r >> 1;
            if (nums[mid] >= nums[0]) l = mid + 1;
            else r = mid;
        }
        return nums[l];
    }
};

19 评论

cxposition 2023-02-17 11:31

打卡(原汁原味)

class Solution {
public:
    int findMin(vector<int>& nums) {
        if (nums.size() == 1) return nums[0];
        int l = 0, r = nums.size() - 1;
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (nums[mid] >= nums[0]) l = mid;
            else r = mid - 1;
        }
        return nums[(r + 1) % nums.size()];
    }
};

Charon 2019-07-29 16:44

大佬有没有不使用 if (nums.back() > nums[0]) return nums[0]; 也可以过得方法？

yxc 2019-08-01 11:04

可以的，判断的性质改成 nums[mid] <= nums.back() 就可以了。可以参考这份代码 LeetCode 153. Find Minimum in Rotated Sorted Array

林慢慢 2022-09-01 10:58

比较的是右端点，有序的情况不用特判。

class Solution {
public:
    int findMin(vector<int>& nums) {
        int l = 0, r = nums.size() - 1;
        while(l < r)
        {
            int mid = l + r >> 1;
            if (nums[mid] < nums[r]) r = mid;
            else l = mid + 1;
        }
        return nums[r];
    }
};

lovestudykid 2021-08-12 06:39

这里超出了前面总结的二分法模板。模板一是找第一个满足条件的，模板二是找最后一个满足条件的。这里是找第一个不满足条件的。改成模板一用nums[0]<nums[mid]应该结果一样的。

吕德华 2019-07-12 12:32

大佬，我这个为什么runtime error呢？

class Solution{
public:
    int findMin(vector<int>& nums)
    {
       if(nums.back()>nums[0]) return nums[0];
       int l=0,r=nums.size()-1;
       while(l<r)
       {
        int mid=l+r+1>>1;
        if(nums[mid]>=nums[0]) l=mid;
        else r=mid-1;
       }
       return nums[r+1];
    }
};

yxc 2019-07-13 10:33

二分结束后，当r = nums.size() - 1的时候，nums[r + 1会数组越界

吕德华 2019-07-13 11:42 回复了 yxc 的评论

明白了，感谢大佬的指教

Jax 2019-07-09 10:07

请问如果判断条件是 mid位置上的数小于等于最右端的数的话，这样是不是就不用考虑完全单调的情况啦，好像是这样哈哈哈

yxc 2019-07-09 15:08

啊对滴，这样可以少写个判断hh

yxc 2019-07-08 21:35

区间更新方式有两种：

l = mid + 1; r = mid;
l = mid; r = mid - 1;

如果是第一种，mid就不加1；如果是第二种，mid就需要加上1。

Egqawkq 2021-03-04 17:29

class Solution {
public:
    int findMin(vector<int>& nums) {
        if (nums.back() > nums[0]) return nums[0];
        int l = 0, r = nums.size() - 1;
        while (l < r)
        {
            int mid = (l + r + 1) >> 1;
            if(nums[mid] > nums[0]) l = mid ;
            else r = mid  - 1;
        }
        return nums[l];
    }
};

y总，为什么用第二种模板无法AC？

lovestudykid 2021-08-12 06:40 回复了 Egqawkq 的评论

应该是nums[mid] >= nums[0]

cll27 2023-07-27 12:54 回复了 lovestudykid 的评论

nums[mid] >= nums[0] 加上也不对啊我的哥

xmvim 2个月前回复了 lovestudykid 的评论

if(nums[mid] > nums[0]) l = mid ; 需要改成 l=mid+1。nums[0] 属于较大的一侧，mid 位置已经大于了 nums[0]，那么分界点肯定就不在这一段上，分界点所在区间不应该包含 mid 这个位置，所以下一次需要在 l = mid+1。你这样写，在旋转的情况下，反而枚举出了最大值hh