题目描述

二叉搜索树中的某两个节点的值被错误地交换了，请在不改变二叉搜索树结构的条件下，恢复出交换前的树。
注意：只能使用额外 $O(1)$ 的空间。

样例1

输入：[1,3,null,null,2]

   1
  /
 3
  \
   2

输出：[3,1,null,null,2]

   3
  /
 1
  \
   2

样例2

输入：[3,1,4,null,null,2]

  3
 / \
1   4
   /
  2

输出：[2,1,4,null,null,3]

  2
 / \
1   4
   /
  3

算法

(Morris-traversal) $O(n)$

这道题目如果用递归做，递归的层数最坏是 $O(n)$ 级别的，所以系统栈的空间复杂度是 $O(n)$，与题目要求的 $O(1)$ 额外空间不符。
同理用栈模拟递归的迭代方式的空间复杂度也是 $O(n)$，不符合题目要求。

这道题目可以用Morris-traversal算法，该算法可以用额外 $O(1)$ 的空间，以及 $O(n)$ 的时间复杂度，中序遍历一棵二叉树。

Morris-traversal 算法流程：
下图给了一个具体示例：

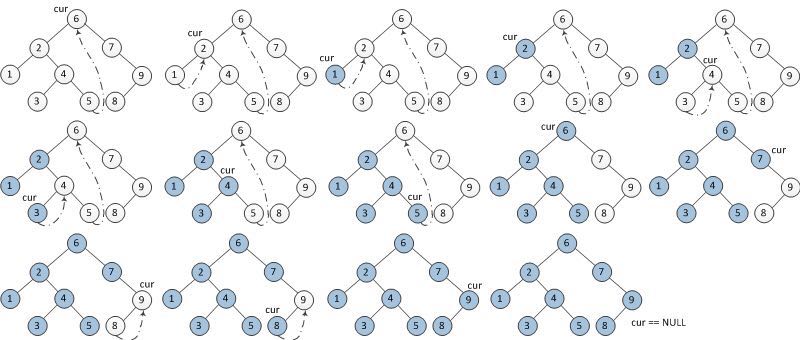
从根节点开始遍历，直至当前节点为空为止：

1. 如果当前节点没有左儿子，则打印当前节点的值，然后进入右子树；
2. 如果当前节点有左儿子，则找当前节点的前驱。
   (1) 如果前驱节点的右儿子为空，说明左子树没遍历过，则进入左子树遍历，并将前驱节点的右儿子置成当前节点，方便回溯；
   (2) 如果前驱节点的右儿子为当前节点，说明左子树已被遍历过，则将前驱节点的右儿子恢复为空，然后打印当前节点的值，然后进入右子树继续遍历；

中序遍历的结果就是二叉树搜索树所表示的有序数列。有序数列从小到大排序，但有两个数被交换了位置。共有两种情况：

1. 交换的是相邻两个数，例如 1 3 2 4 5 6，则第一个逆序对，就是被交换的两个数，这里是3和2；
2. 交换的是不相邻的数，例如 1 5 3 4 2 6，则第一个逆序对的第一个数，和第二个逆序对的第二个数，就是被交换的两个数，这里是5和2；

找到被交换的数后，我们将它们换回来即可。

复杂度分析：Morris-traversal算法的时间复杂度是 $O(n)$，额外空间复杂度是 $O(1)$。
这里可能有同学会问，Morris-traversal算法中每次都会求当前节点的前驱节点，而求前驱节点的最坏时间复杂度是 $O(n)$，那遍历整棵树的时间复杂度为什么不是 $O(n^2)$ 呢？这是因为对于一棵二叉树，对所有节点求一遍前驱，则每条边只会被遍历两次，所以时间复杂度加一块也是 $O(n)$。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    void recoverTree(TreeNode* root) {
        TreeNode *first = NULL, *second, *prep = NULL;
        while (root)
        {
            if (!root->left)
            {
                if (prep && prep->val > root->val)
                {
                    if (!first) first = prep, second = root;
                    else second = root;
                }
                prep = root;
                root = root->right;
            }
            else
            {
                TreeNode *p = root->left;
                while (p->right && p->right != root) p = p->right;
                if (!p->right)
                {
                    p->right = root;
                    root = root->left;
                }
                else
                {
                    p->right = NULL;
                    if (prep && prep->val > root->val)
                    {
                        if (!first) first = prep, second = root;
                        else second = root;
                    }
                    prep = root;
                    root = root->right;
                }
            }
        }
        swap(first->val, second->val);
    }
};