题目链接

4313. 满二叉树等长路径

给定一个深度为 $n$ 的满二叉树，其 $2n+1−1$ 个顶点的编号为 $1∼2n+1−1$。

树的根节点为 $1$ 号节点，除根节点外，第 $i$ 号节点的父节点为第 $⌊i_2⌋$ 号节点。

例如，当 $n=3$ 时，二叉树如下所示：

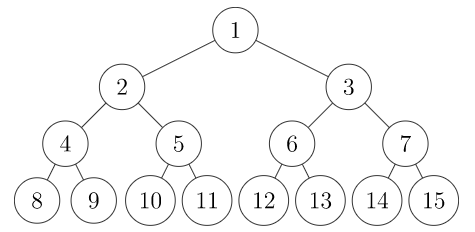
树中每条边的长度已知，由此可以得到根节点到 $2^n$ 个叶节点的距离。

为了使得根节点到每个叶节点的距离都相等，我们可以进行任意次增边操作。

每次操作可以选择任意一条边，将其增加任意正整数长度。

我们希望在达成目的的同时，所有边的总增加长度尽可能小。

请你计算并输出总增加长度的最小可能值。

输入格式

第一行包含整数 $n$。

第二行包含 $2^{n+1}−2$ 个整数 $a_2,a_3,…,a_{2^{n+1}−1}$，其中 $a_i$ 表示第 $i$ 号节点与第 $⌊\frac{i}{2}⌋$ 号节点之间的边的长度。

输出格式

一个整数，表示总增加长度的最小可能值。

数据范围

前三个测试点满足 $1≤n≤2$。
所有测试点满足 $1≤n≤10，1≤a_i≤100$。

输入样例：

2
1 2 3 4 5 6

输出样例：

5

解题思路

贪心

考虑最终每个儿子节点的距离，这个值肯定是大于或等于开始时每个叶子节点的距离的最大值，如果这个值大于开始时的最大值的话显然是通过加上面的边得到的，这个操作显然不如等于最大值好，所以最终距离即为最大值，由上到下增边即可获得最小增边长度

• 时间复杂度：$O(2^n)$

代码

// Problem: 满二叉树等长路径
// Contest: AcWing
// URL: https://www.acwing.com/problem/content/4316/
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

// %%%Skyqwq
#include <bits/stdc++.h>

//#define int long long
#define help {cin.tie(NULL); cout.tie(NULL);}
#define pb push_back
#define fi first
#define se second
#define mkp make_pair
using namespace std;

typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;

template <typename T> bool chkMax(T &x, T y) { return (y > x) ? x = y, 1 : 0; }
template <typename T> bool chkMin(T &x, T y) { return (y < x) ? x = y, 1 : 0; }

template <typename T> void inline read(T &x) {
    int f = 1; x = 0; char s = getchar();
    while (s < '0' || s > '9') { if (s == '-') f = -1; s = getchar(); }
    while (s <= '9' && s >= '0') x = x * 10 + (s ^ 48), s = getchar();
    x *= f;
}

const int N=2050;
int res,n,w[N];
int dfs(int u)
{
    if(u*2>(1<<n+1)-1)return 0;
    int l=w[u*2]+dfs(u*2),r=w[u*2+1]+dfs(u*2+1);
    res+=abs(l-r);
    return max(l,r);
}
int main()
{
    cin>>n;
    for(int i=2;i<=(1<<n+1)-1;i++)cin>>w[i];
    dfs(1);
    cout<<res;
    return 0;
}