题目描述

Given two binary trees original and cloned and given a reference to a node target in the original tree.

The cloned tree is a copy of the original tree.

Return a reference to the same node in the cloned tree.

Note that you are not allowed to change any of the two trees or the target node and the answer must be a reference to a node in the cloned tree.

Follow up: Solve the problem if repeated values on the tree are allowed.

Example 1:

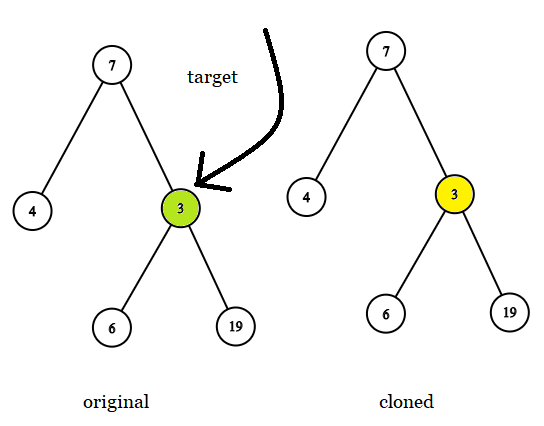
Input: tree = [7,4,3,null,null,6,19], target = 3
Output: 3
Explanation: In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.

Example 2:

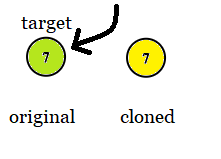
Input: tree = [7], target =  7
Output: 7

Example 3:

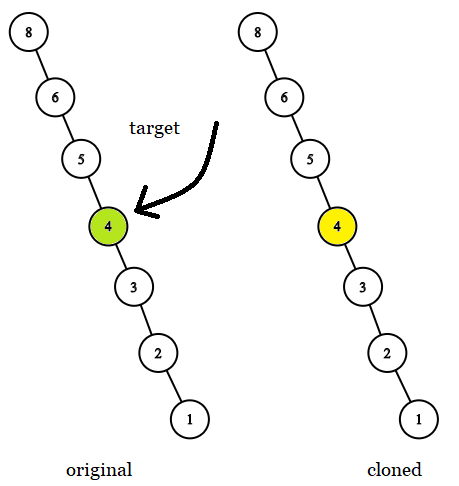
Input: tree = [8,null,6,null,5,null,4,null,3,null,2,null,1], target = 4
Output: 4

Example 4:

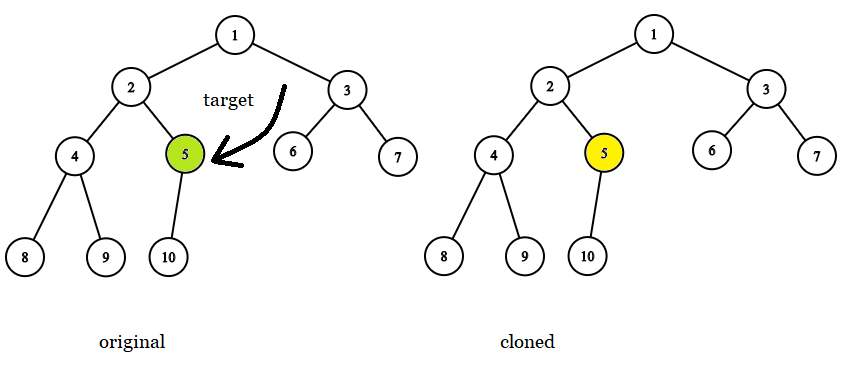
Input: tree = [1,2,3,4,5,6,7,8,9,10], target = 5
Output: 5

Example 5:

Input: tree = [1,2,null,3], target = 2
Output: 2

Constraints:

• The number of nodes in the tree is in the range [1, 10^4].
• The values of the nodes of the tree are unique.
• target node is a node from the original tree and is not null.

题意：给出两棵二叉树original和cloned，并且给出original树中某一个节点target。cloned树是original树的一个深复制，请返回在cloned树中与target节点相对应的节点。

我们不允许改变任何一个节点，而且返回值必须是cloned树中的节点。

请考虑树中有重复值节点的情况。

算法1

(非递归后序遍历)

题解：如果树中没有重复节点的话，那么很简单，我们只需要记录target的值，然后使用任何一种遍历找到值相等的节点即可。有重复节点的话，问题会稍微困难一些，但是我们知道二叉树有一个很重要的特性：当使用后序遍历到某一个节点时，栈中的所有节点就是从根节点到当前节点的路径。因此，我们可以先在original树中使用后序遍历找到target节点，然后根据路径判断从original到target的每一步是向左还是向右。我们在cloned树中使用同样的方向即可。

    TreeNode* getTargetCopy(TreeNode* original, TreeNode* cloned, TreeNode* target) {
        //  二叉树非递归后序遍历
        stack<TreeNode*> st_node;
        stack<int> st_vis;
        TreeNode* cur = original;
        while(!st_node.empty() || cur != NULL)
        {
            while(cur != NULL)
            {
                st_node.push(cur);
                st_vis.push(0);
                cur = cur->left;
            }
            TreeNode* p = st_node.top();
            if(st_vis.top() == 0)
            {
                st_vis.top() = 1;
                cur = p->right;
            }else{
                if(p == target)
                    break;
                st_vis.pop();
                st_node.pop();
            }
        }
        //  根据遍历结果还原每一步的方向，0代表左儿子，1代表右儿子
        vector<int> dir;
        while(!st_node.empty())
        {
            TreeNode* p = st_node.top();
            st_node.pop();
            if(!st_node.empty())
            {
                if(p == st_node.top()->left)
                    dir.push_back(0);
                else
                    dir.push_back(1);
            }
        }
        //  根据方向数组找到对应的节点
        TreeNode* res = cloned;
        for(int i = dir.size() - 1 ; i >= 0 ; i --)
        {
            if(dir[i] == 0) res = res->left;
            else res = res->right;
        }
        return res;
    }