题目描述

On a 2 dimensional grid with R rows and C columns, we start at (r0, c0) facing east.

Here, the north-west corner of the grid is at the first row and column, and the south-east corner of the grid is at the last row and column.

Now, we walk in a clockwise spiral shape to visit every position in this grid.

Whenever we would move outside the boundary of the grid, we continue our walk outside the grid (but may return to the grid boundary later.)

Eventually, we reach all R * C spaces of the grid.

Return a list of coordinates representing the positions of the grid in the order they were visited.

Example 1:

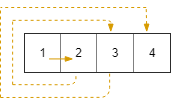
Input: R = 1, C = 4, r0 = 0, c0 = 0
Output: [[0,0],[0,1],[0,2],[0,3]]

Example 2:

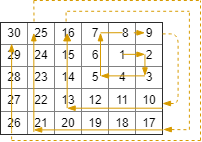
Input: R = 5, C = 6, r0 = 1, c0 = 4
Output: [[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]

Note:

1. 1 <= R <= 100
2. 1 <= C <= 100
3. 0 <= r0 < R
4. 0 <= c0 < C

题意：在 R 行 C 列的矩阵上，我们从 (r0, c0) 面朝东面开始

这里，网格的西北角位于第一行第一列，网格的东南角位于最后一行最后一列。

现在，我们以顺时针按螺旋状行走，访问此网格中的每个位置。

每当我们移动到网格的边界之外时，我们会继续在网格之外行走（但稍后可能会返回到网格边界）。

最终，我们到过网格的所有 R * C 个空间。

按照访问顺序返回表示网格位置的坐标列表。

算法1

题解：我们观察到在每个方向上走过的步长为1，1，2，2，3，3，。。。并且每次走完一定的步长都需要右转90度。我们对走过的每一个坐标进行模拟即可，只有当坐标在网格内部才记录答案。

    vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) {
        // cnt：已经访问的网格数，tar：总共需要访问的网格数，cur:当前循环内的步长
        //  st:当前方向，dx,dy为方向数组
        int st = 0,dx[4] = {0,1,0,-1},dy[4] = {1,0,-1,0},cnt = 0,tar = R * C;
        vector<vector<int>> res;
        int cur = 1;
        while(cnt < tar)
        {
            res.push_back(r0,c0);
            for(int i = 0 ; i < cur ; i ++)
            {
                r0 += dx[st],c0 += dy[st];
                if(r0 >= 0 && r0 < R && c0 >= 0 && c0 < C)
                {
                    res.push_back({r0,c0});
                    cnt ++;
                }
            }
            st = (st + 1) % 4;
            for(int i = 0 ; i < cur ; i ++)
            {
                r0 += dx[st],c0 += dy[st];
                if(r0 >= 0 && r0 < R && c0 >= 0 && c0 < C)
                {
                    res.push_back({r0,c0});
                    cnt ++;
                }
            }
            cur ++ ;
        }
        return res;
    }