思路分析

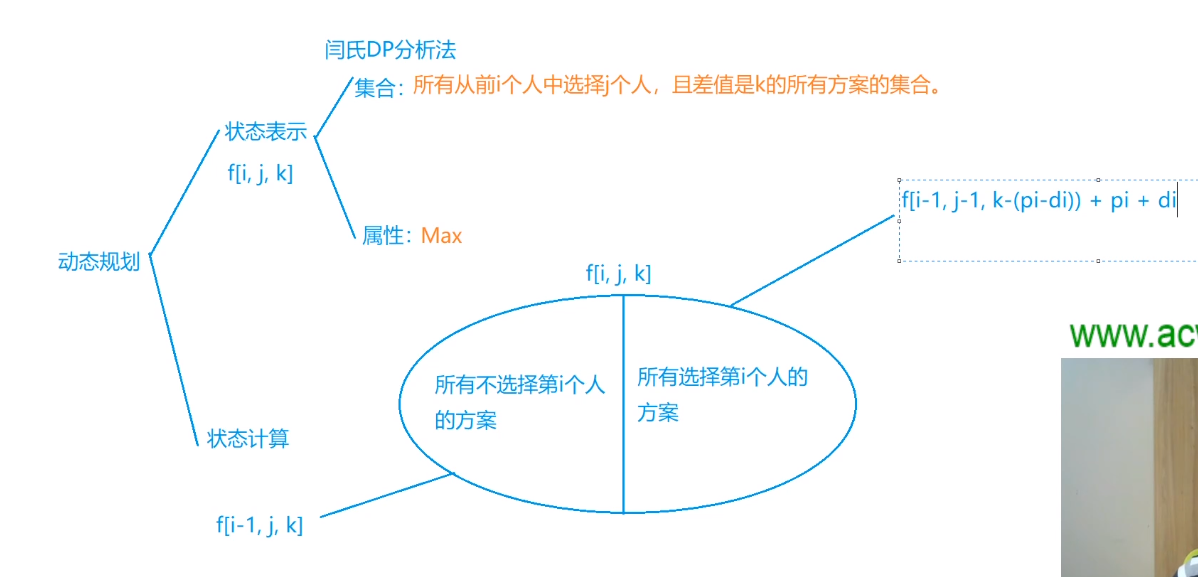
本题细节很多，不容易做对，简单说下思路，本题是一道具有多个体积维度的01背包问题， 人数限制m个是一个体积，控方和辩方的总分的差值是一个体积，所以就可以按照01背包的状态表示方式写出本题的状态表示，下面的图片中有写，还需要分析出来的就是 差值的范围 是-400 到 400 之间，因为下标不能为负数，所以我们可以加一个偏移量400，这样就映射到了0 到 800之间，且不影响差值之间的大小关系，因为每一个偏移量都加了400，剩下的就是细节处理，这个得写之后才能发现

C++ 代码

#include <bits/stdc++.h>
using namespace std;

const int N = 210, M = 21, base = 400;//偏移量

int p[N];
int d[N];
int dp[N][M][810];//从前i个人中已经选了j个人，差值的为k的最大价值
int n, m;

int main(){
    int T = 1;
    while(cin >> n >> m, n || m){
        for(int i = 1;i <= n;++i){
            cin >> p[i] >> d[i];
        }

        memset(dp, -0x3f, sizeof dp);
        dp[0][0][base] = 0;

        for(int i = 1;i <= n;++i)
            for(int j = 0;j <= m;++j)
                for(int k = -400;k <= 400;++k){
                    dp[i][j][k+base] = dp[i-1][j][k+base];//不选第i个
                    int t = k+base - (p[i] - d[i]);
                    if(t < 0 || t > 800) continue;
                    if(j < 1) continue;//j必须从0开始 否则不对
                    dp[i][j][k+base] = max(dp[i][j][k+base], dp[i-1][j-1][t] + p[i] + d[i]);//选第i个              
                }

        int v = 0;//加上偏移量后的差值
        while (dp[n][m][base - v] < 0 && dp[n][m][base + v] < 0) v ++ ;//找到差值最小的
        v = (dp[n][m][base+v] > dp[n][m][base-v] ? base + v : base - v);//找到差值相同时价值最大的

        //反推求方案
        vector<int> ans;
        int i = n, j = m, k = v;
        while(j){
            if(dp[i][j][k] == dp[i-1][j][k]){
                i -= 1;
            }else{
                ans.push_back(i);
                k -= (p[i] - d[i]);
                i -= 1;
                j -= 1;
            }
        }

        //求控方总分和辩方总分
        int sp = 0, sd = 0;
        for(int i = 0;i < ans.size();++i){
            sp += p[ans[i]];
            sd += d[ans[i]];
        }
        sort(ans.begin(), ans.end());
        //输出答案
        printf("Jury #%d\n", T ++ );
        printf("Best jury has value %d for prosecution and value %d for defence:\n", sp, sd);
        for (int i = 0; i < ans.size(); i ++ ) printf(" %d", ans[i]);
        puts("\n");

    }
}