题目描述

给你一棵由 n 个顶点组成的无向树，顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下：

• 在一秒内，青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点（如果它们直接相连）。

• 青蛙无法跳回已经访问过的顶点。

• 如果青蛙可以跳到多个不同顶点，那么它跳到其中任意一个顶点上的机率都相同。

• 如果青蛙不能跳到任何未访问过的顶点上，那么它每次跳跃都会停留在原地。

无向树的边用数组 edges 描述，其中 edges[i] = [fromi, toi] 意味着存在一条直接连通 fromi 和 toi 两个顶点的边。

返回青蛙在 t 秒后位于目标顶点 target 上的概率。

样例

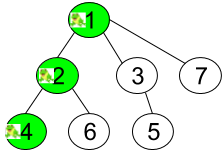
输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
输出：0.16666666666666666 
解释：上图显示了青蛙的跳跃路径。
青蛙从顶点 1 起跳，第 1 秒 有 1/3 的概率跳到顶点 2 ，然后第 2 秒 有 1/2 的概率跳到顶点 4。
因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。 

输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
输出：0.3333333333333333
解释：上图显示了青蛙的跳跃路径。
青蛙从顶点 1 起跳，有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。 

输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 20, target = 6
输出：0.16666666666666666

提示：

• 1 <= n <= 100 edges.length == n-1

• edges[i].length == 2

• 1 <= edges[i][0], edges[i][1] <= n

• 1 <= t <= 50

• 1 <= target <= n

• 与准确值误差在 10^-5 之内的结果将被判定为正确。

算法分析

• 1、先建图，预处理road[]数组，road[i]表示从i点往下走有多少条路，不能往回走

• 2、ans[i]表示到达i点的概率的倒数，即该点的概率为1 / ans[i]

• 3、通过深度优先遍历，算出走到每个点在当前深度的概率，res是目标点的概率，枚举到目标结点

  • 若该点深度大于t，则return

  • 若该点深度等于t，则赋值res = 1.0 / ans[u]

  • 若该点深度小于t且该节点已经没有子结点，表示永远都会停到该点，则赋值res = 1.0 / ans[u]

时间复杂度 $O(n)$

Java 代码

class Solution {
    static int N = 110,M = N * 2;
    static int[] h = new int[N];
    static int[] e = new int[M];
    static int[] ne = new int[M];
    static int idx = 0;
    static int[] road = new int[N];//每个点有多少条路径
    static double[] ans = new double[N];
    static double res = 0;
    static void add(int a,int b)
    {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx ++;
    }

    //找每个点有多少条路径
    static void dfs_r(int u,int father)
    {
        int cnt = 0;
        for(int i = h[u];i != -1;i = ne[i])
        {
            int j = e[i];
            if(j == father) continue;
            cnt ++;
            dfs_r(j,u);
        }
        road[u] = cnt;
    }

    static void dfs(int u,int father,int depth,int t,int target)
    {
        if(depth > t) return;
        if(depth == t && u == target) res = 1.0 / ans[u];
        boolean flag = false;//标记往下是否有节点,初始为false
        for(int i = h[u];i != -1;i = ne[i])
        {
            int j = e[i];
            if(j == father) continue;
            flag = true;
            ans[j] = ans[u] * road[u];

            dfs(j,u,depth + 1,t,target);
        }
        if(!flag && u == target)  res = 1.0 / ans[u];
    }
    public double frogPosition(int n, int[][] edges, int t, int target) {
        res = 0;
        idx = 0;
        Arrays.fill(h,-1);
        for(int i = 0;i < edges.length;i ++)
        {
            int a = edges[i][0];
            int b = edges[i][1];
            add(a,b);
            add(b,a);
        }
        dfs_r(1,-1);
        ans[1] = 1;
        dfs(1,-1,0,t,target);
        return res;
    }
}