https://www.acwing.com/problem/content/6/

v[i](下面都简写成v)表示第i个物品体积,其中j=v-1,m表示背包最大容量。这里我们假设m=kv+j,其实也有可能是kv+j-1,…,kv+1,kv 只是为了方便下面的这个矩形演示,不妨假设成m=kv+j。
| dp[0] | dp[v] | dp[2v] | dp[3v] | … | dp[(k-1)v] | dp[kv] |
| dp[1] | dp[v+1] | dp[2v+1] | dp[3v+1] | … | dp[(k-1)v+1] | dp[kv+1] |
| dp[2] | dp[v+2] | dp[2v+2] | dp[3v+2] | … | dp[(k-1)v+2] | dp[kv+2] |
| dp[3] | dp[v+3] | dp[2v+3] | dp[3v+3] | … | dp[(k-1)v+3] | dp[kv+3] |
| … | … | … | … | … | … | … |
| dp[j-1] | dp[v+j-1] | dp[2v+j-1] | dp[3v+j-1] | … | dp[(k-1)v+j-1] | dp[(kv+j-1)] |
| dp[j] | dp[v+j] | dp[2v+j] | dp[3v+j] | … | dp[(k-1)v+j] | dp[kv+j] |
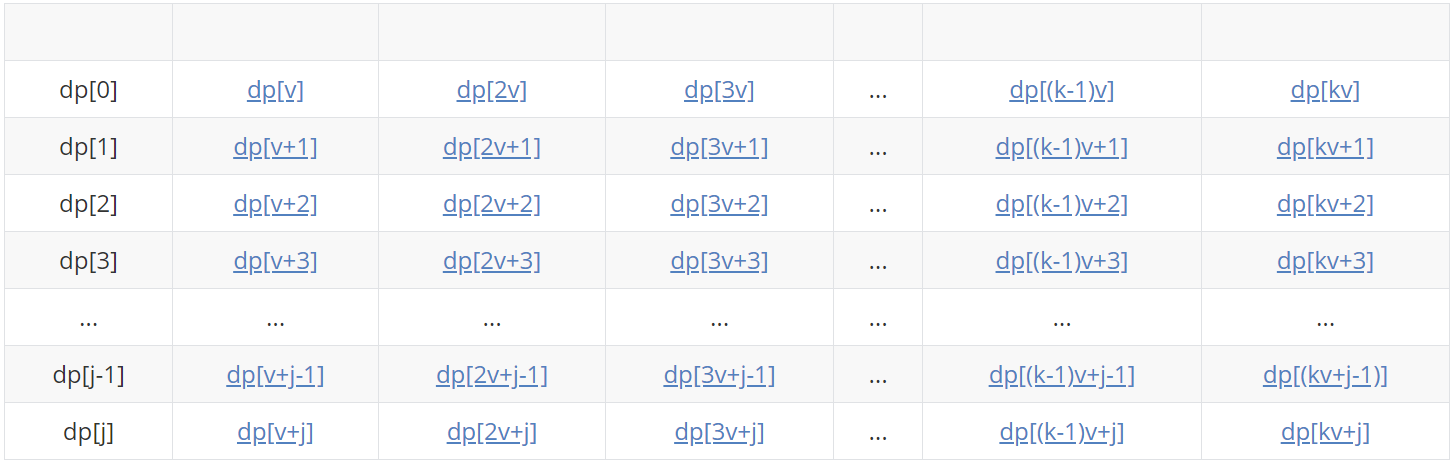
回顾一下多重背包问题Ⅰ和Ⅱ所提及的解法,在代码中的实现的第二层循环的dp都是这个状态转移流程:对于每一个物品i,都会从大到小枚举值在[v,m]的所有情况都进行一遍更新(标蓝的元素),枚举的顺序如下图示:
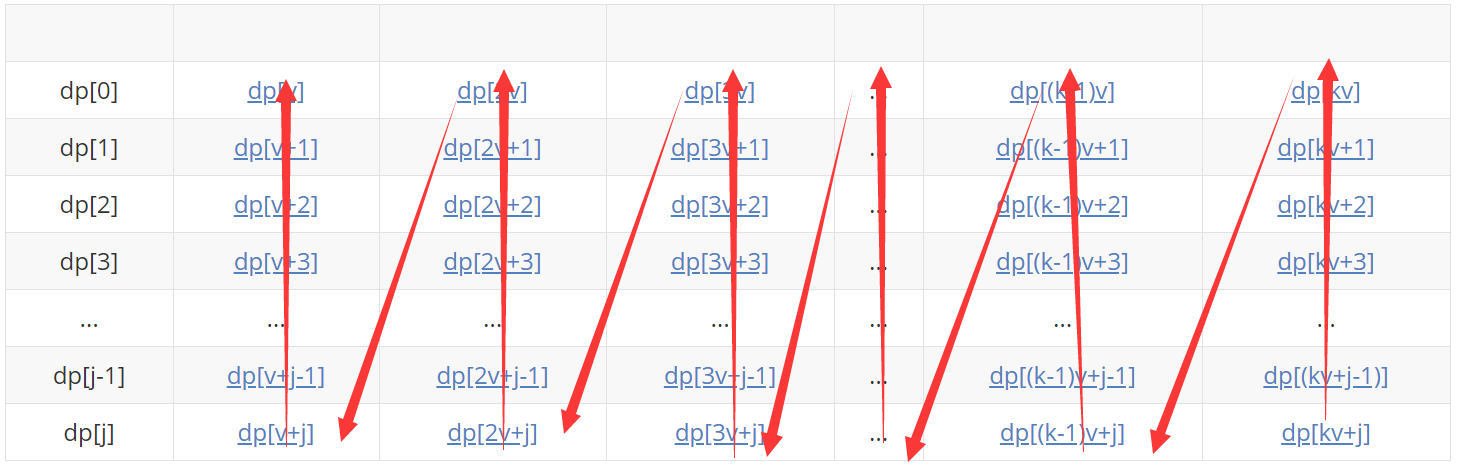
下面做具体分析:
其中标蓝元素代表待更新的状态(需要取max),粗体代表能转移到待更新状态的状态(当然,由于物品个数的限制,可能没有k个,不会是这么长,这里只是为了方便演示,暂不考虑物品个数)

dp[kv+j]=max( dp[(k-1)v+j] + w , dp[(k-2)v+j] + 2w , ... , dp[3v+j] + (k-3)w , dp[2v+j] + (k-2)w , dp[v+j] + (k-1)w , dp[j] + kw )

......
......
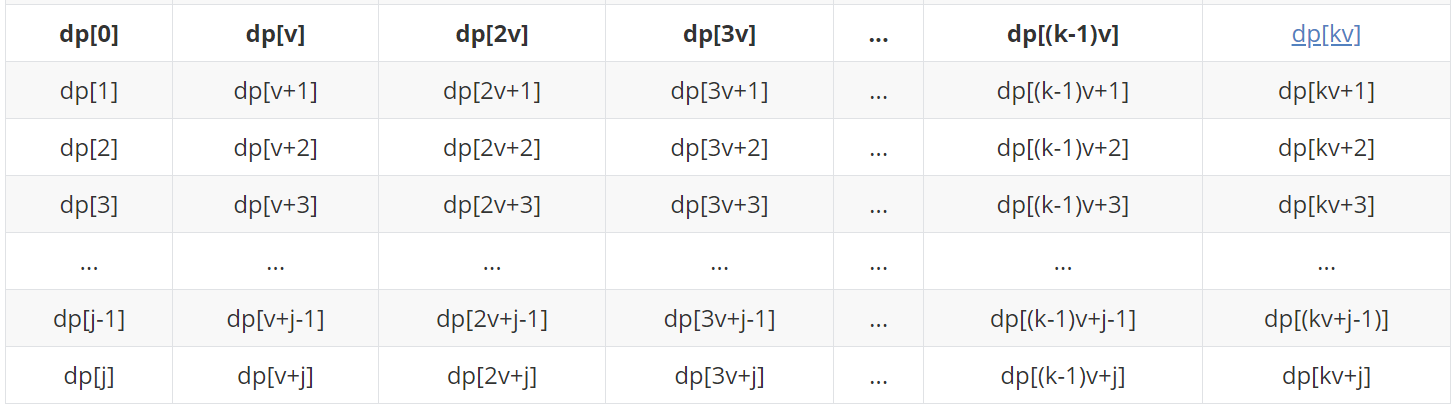

dp[(k-1)v+j]=max( dp[(k-2)v+j] + w , ... , dp[3v+j] + (k-4)w , dp[2v+j] + (k-3)w , dp[v+j] + (k-2)w , dp[j] + (k-1)w )
到这里的时候对比上图和下图,细心的你突然发现这里好像进行了很多没必要(貌似重复冗余但又不得不做的工作)的比较,下面进行分析:
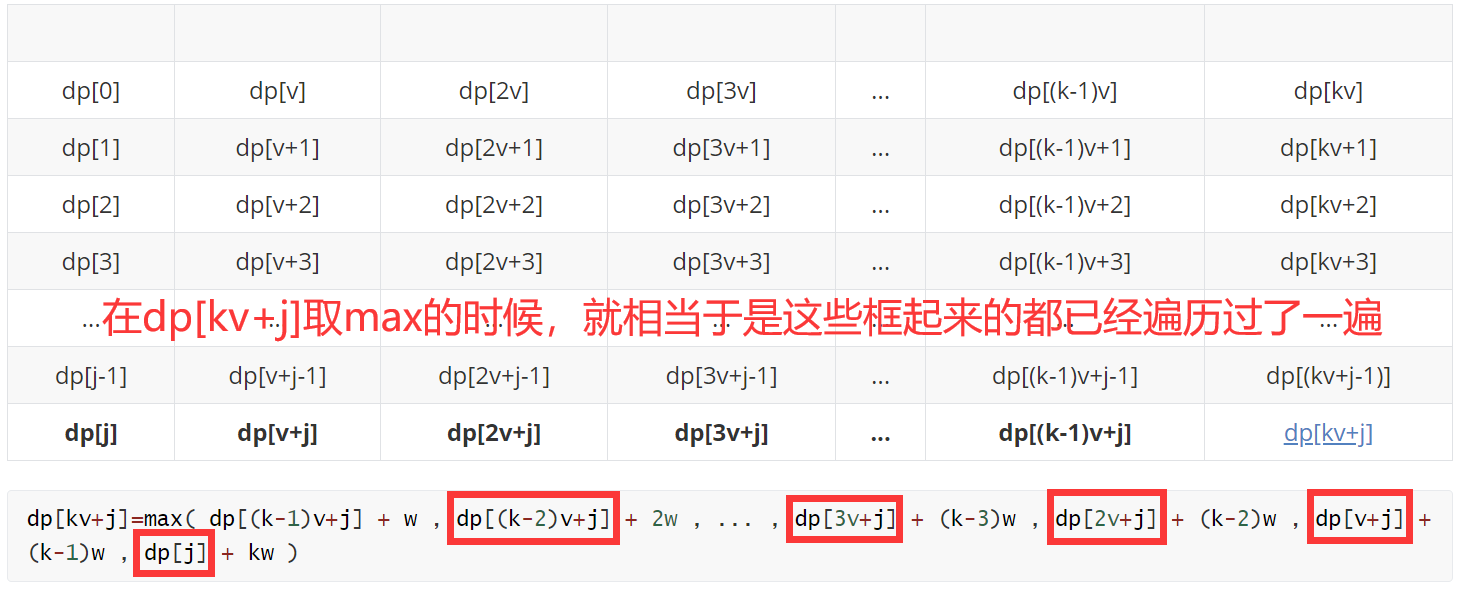
而我们在进行dp[(k-1)v+j]的状态更新(取max)的时候又重新将它们再遍历了一遍。
问题出在:我们每次取max都需要从“0”开始对集合(同一行)内的所有元素比较,而不能在之前的比较结果的基础上进行。
导致问题的原因:我们是从大到小枚举的。举个例子:这就相当于我们遍历一个正整数集合,得到这个集合的最大值,然后我们从集合中剔除一个元素,新集合的最大值对于我们来说不是确定的(细品),我们无法利用上一次的遍历所做的工作(劳动成果不能为这次所用)。
思考:如果做逆向思维,我们遍历一个正整数集合,得到这个集合的最大值,然后我们往集合中增加一个元素,新集合的最大值对于我们来说是确定的,我们可以利用上一次的遍历所做的工作(劳动成果能够为这次所用)。
解决方法:所以我们应该摒弃前文描述的“从大到小枚举压缩空间”的思想,选择从小到大枚举,并且利用一种数据结构来模拟这个“变大的集合”,并且在此基础上做一些限制条件实现物品个数的限制。由于只有差值为v的时候状态才能转移,我们可以把整个集合以模v的余数为划分规则做一个等价划分,可以划分成为v个子集(模v余[0, v-1] 则每行代表一个子集,这也是本文设计这个矩形的目的),这个时候我们分别对每个集合从小到大(状态更新,在下表中从左往右)进行枚举更新,还要考虑物品的个数。
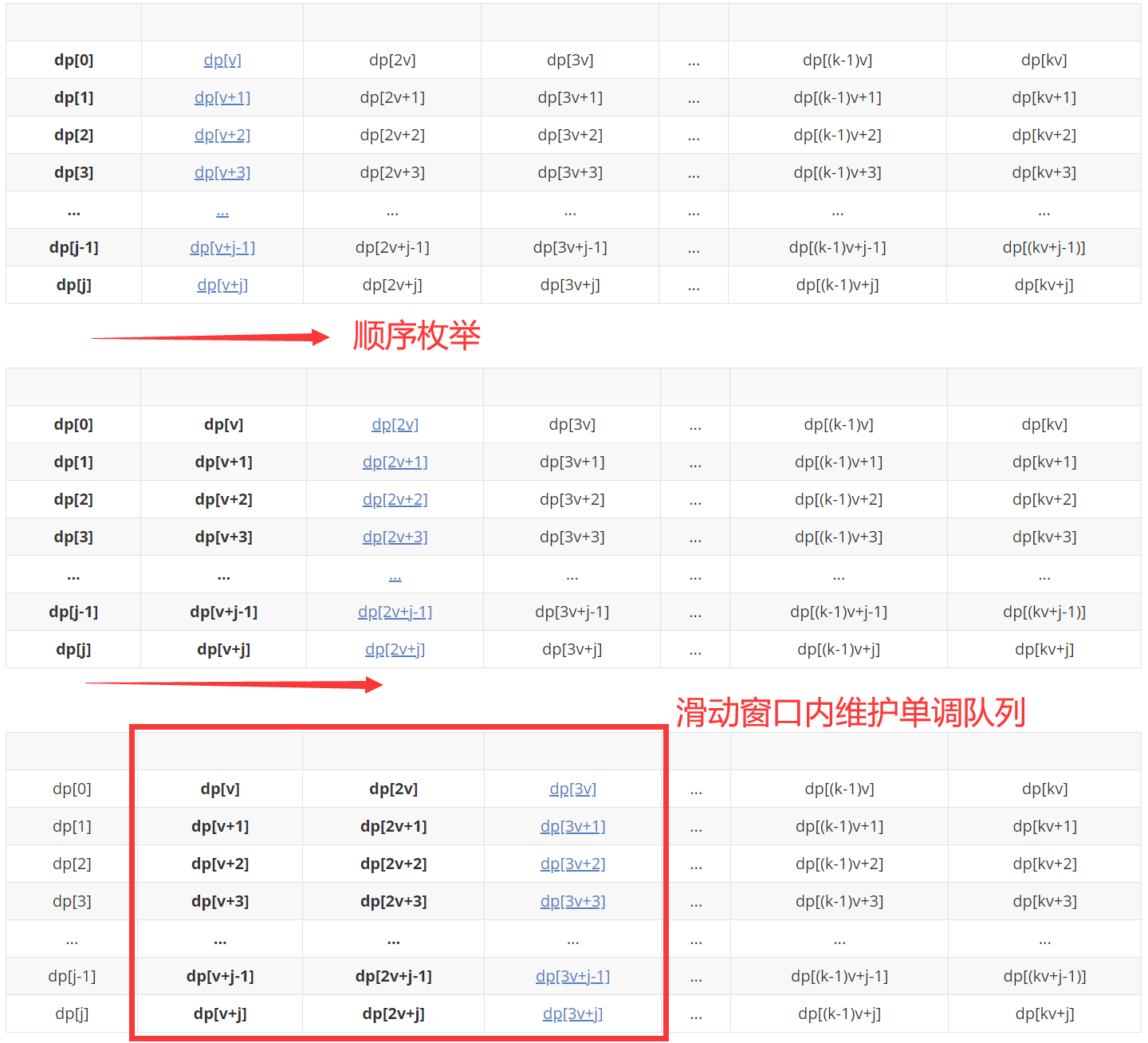
具体实施:以一行(同余的一个子集)为例,设置一个滑动窗口,窗口大小设置为该物品的个数+1,并在窗口内部维护一个单调队列。
至于为什么窗口大小是该物品的个数+1,举个例子:如果该物品只有2个,dp[3v+j]从dp[j]状态转移过来需要装进来3个该物品,所以不可能从dp[j]转移过来,因此也就没有必要去将dp[j]考虑进来,只需要维护窗口大小为3范围内的单调队列。

首先解释一下单调队列:
顾名思义,单调队列的重点分为 "单调" 和 "队列"
"单调" 指的是元素的的 "规律"——递增(或递减)
"队列" 指的是元素只能从队头和队尾进行操作,但是此"队列" 非彼队列。
如果要求每连续的k个数中的最大值,很明显,当一个数进入所要 “寻找” 最大值的范围中时,若这个数比其前面(先进队)的数要大,显然,前面的数会比这个数先出队且不再可能是最大值。
也就是说——当满足以上条件时,可将前面的数 “踢出”,再将该数push进队尾。
这就相当于维护了一个递减的队列,符合单调队列的定义,减少了重复的比较次数(前面的“劳动成果”能够为后面所用),不仅如此,由于维护出的队伍是查询范围内的且是递减的,队头必定是该查询区域内的最大值,因此输出时只需输出队头即可。显而易见的是,在这样的算法中,每个数只要进队与出队各一次,因此时间复杂度被降到了O(N)。
如果对于文字解释看不懂也没关系,结合模拟来介绍:假设物品个数为2,则窗口大小为3,进行模拟。在这个过程中,因为我们是从小到大进行更新,所以需要对dp的i-1状态备份一份到g中(空间换时间)。
首先给g[j]入队列尾,此时,单调队列中只有g[j],用队头g[j]更新dp[j]:

dp[j]更新之后变成i时候的状态,这里我们假定(g[j]+w > g[v+j])。
g[v+j]入队之前,先从队尾起,把统统不比它大的都踢出队列,然后再入队尾(g[j]+w比它大,踢不掉)。
取队头g[j]+w更新dp[v+j]:
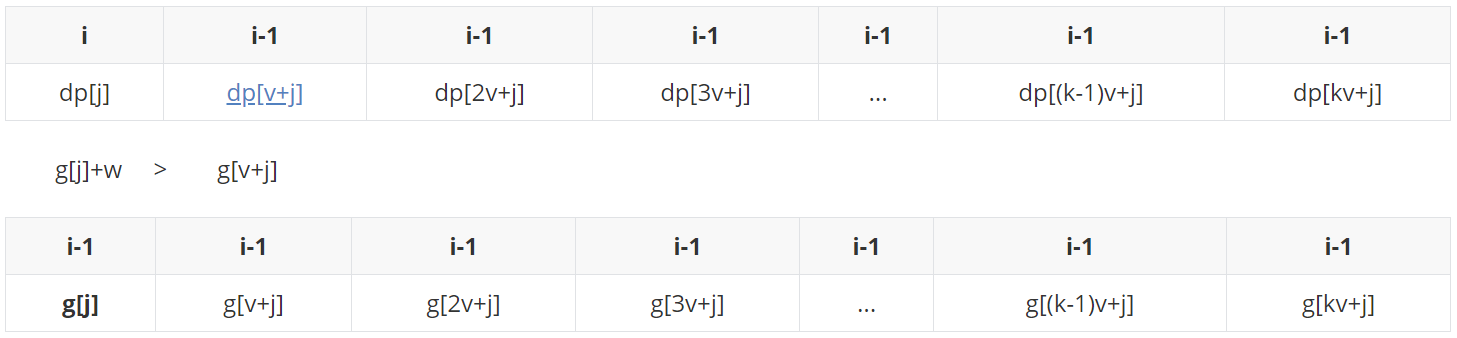
dp[v+j]更新之后变成i时候的状态。
(情况一)如果(g[j]+2w > g[v+j]+w > g[2v+j] )。
g[2v+j]入队之前,先从队尾起比较,发现队尾比它大,踢不了,然后乖乖入队尾。
此时,取队头g[j]+2w更新dp[2v+j]:
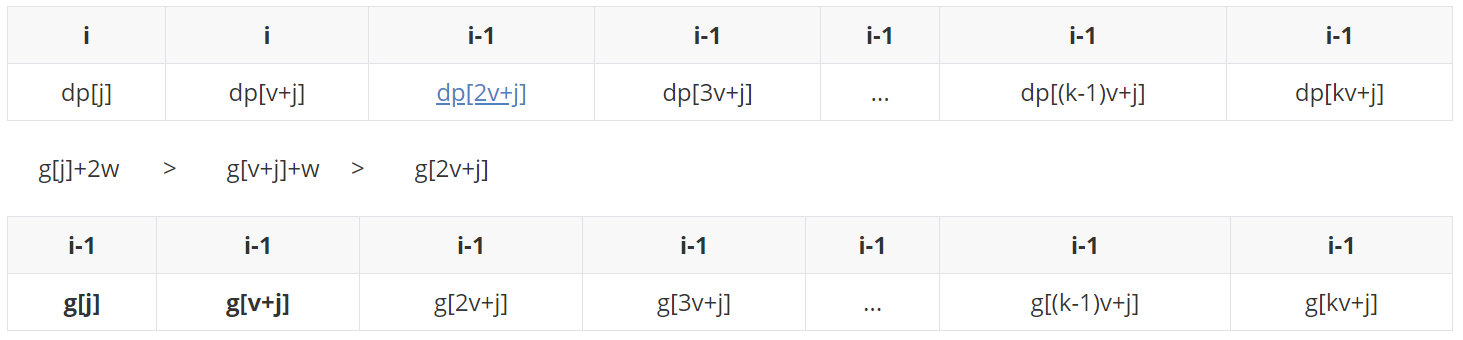
(情况二)如果(g[j]+2w > g[2v+j] >= g[v+j]+w)。
g[2v+j]入队之前,发现队尾的g[v+j]+w不比它大,踢掉了,然后再比较此时的队尾g[j]+2w,比它大,乖乖入队尾。
此时,还是取队头g[j]+2w更新dp[2v+j]:

(情况三)如果(g[2v+j] >= g[j]+2w > g[v+j]+w)。
g[2v+j]入队之前,发现队尾的g[v+j]+w不比它大,踢掉了,然后再比较此时的队尾g[j]+2w,也不比它大,踢掉。此时队列为空,它进入队列。
此时,则取队头g[2v+j]更新dp[2v+j]:

假定我们是以上面三种中的第一种情况( g[j]+2w > g[v+j]+w > g[2v+j] )结束的:

dp[2v+j]更新之后变成i时候的状态。
g[2v+j]入队之前,检查单调队列内的元素是否都在窗口(长度为3)之内,发现g[j]+3w不在,则踢掉,然后......
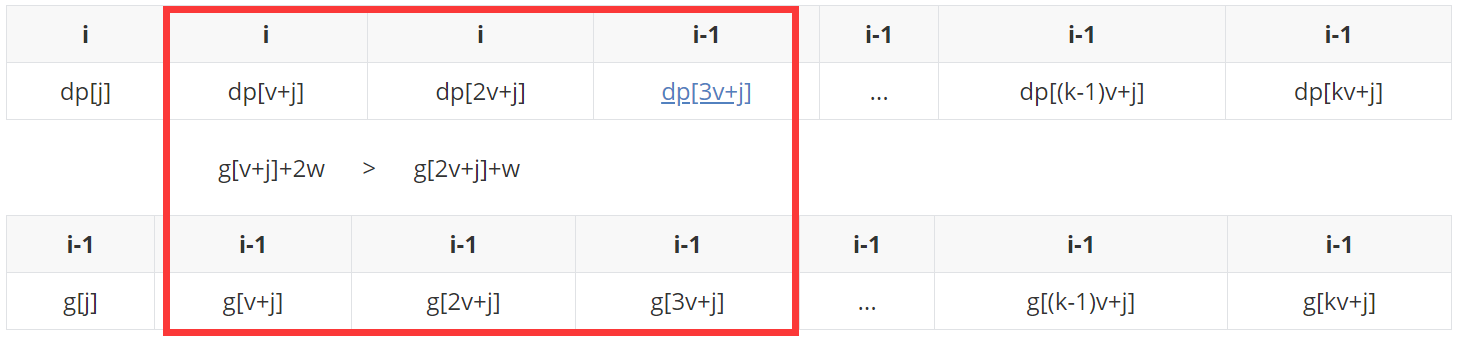
至此,在本次问题中单调队列维护的规则和思路都已经演示清楚,下面直接上代码:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
//多重背包问题: 限制每种物品可取次数
//究极优化:单调队列
const int M = 20010, N = 1010;
int n, m;
int dp[M], g[M];
int que[M]; //队列只存储在同余的集合中是第几个,不存储对应值
int main() {
cin >> n >> m;
for(int i = 0; i < n; i ++){
int v, w, s;
cin >> v >> w >> s;
//复制一份副本g,因为这里会是从小到大,不能像0-1背包那样从大到小,所以必须申请副本存i-1状态的,不然会被影响
memcpy(g, dp, sizeof dp);
for(int r = 0; r < v; r ++) { //因为只有与v同余的状态 相互之间才会影响,余0,1,...,v-1 分为v组
int head = 0, tail = -1;
for(int k = 0; r + k * v <= m; k ++) { //每一组都进行处理,就相当于对所有状态都处理了
//队头不在窗口里面就踢出(队头距离要更新的dp超过了最大个数s,尽管它再大也要舍去,因为达不到)
if(head <= tail && k - que[head] > s) head++;
//这第k个准备进来,把不大于它的队尾统统踢掉,也是为了保持队列的单调降(判断式实际上是两边同时减去了k * w)
//实际意义应该是 g[r + k * v] >= g[r + que[tail] * v] + (k - que[tail]) * w 为判断条件
while(head <= tail && g[r + k * v] - k * w >= g[r + que[tail] * v] - que[tail] * w) tail --;
que[++ tail] = k; //将第k个入列,队列只存储在同余中是第几个,不存储对应值
//余r的这组的第k个取队头更新,队头永远是使之max的决策
dp[r + k * v] = g[r + que[head] * v] + (k - que[head]) * w;
}
}
}
cout << dp[m] << endl;
return 0;
}
时间复杂度:
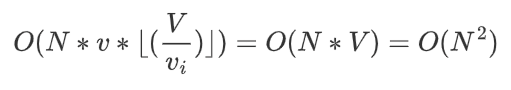
以上内容如有错误的地方,恳请指正。

