题目描述

给你一棵以 root 为根的二叉树，二叉树中的交错路径定义如下：

• 选择二叉树中 任意 结点和一个方向（左或者右）。
• 如果前进方向为右，那么移动到当前结点的的右子结点，否则移动到它的左子结点。
• 改变前进方向：左变右或者右变左。
• 重复第二步和第三步，直到你在树中无法继续移动。

交错路径的长度定义为：访问过的结点数目减一（单个结点的路径长度为 0 ）。

请你返回给定树中最长 交错路径 的长度。

样例

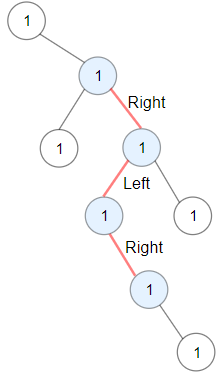
输入：root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
输出：3
解释：蓝色结点为树中最长交错路径（右 -> 左 -> 右）。

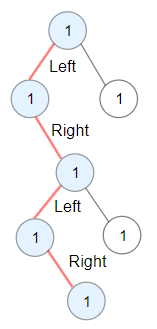
输入：root = [1,1,1,null,1,null,null,1,1,null,1]
输出：4
解释：蓝色结点为树中最长交错路径（左 -> 右 -> 左 -> 右）。

输入：root = [1]
输出：0

限制

• 每棵树最多有 50000 个结点。
• 每个结点的值在 [1, 100] 之间。

算法

(递归) $O(n)$

1. 定义递归函数 solve：接受两个参数，一个当前结点，一个是到当前结点最后一次的方向（0 表示上一次走了左子结点，1 表示上一次走了右子结点），返回以当前结点为起点的最长路径。
2. 在函数中，如果当前结点为空则返回 0。否则，先分别递归左右子结点，得到返回值。全局变量需要记录下以两个子结点作为起点的最大值，作为备选答案。
3. 如果方向为 0，则返回 1 加上右子结点的值；否则，返回 1 加上递归左子结点的值。

时间复杂度

• 每个结点仅遍历一次，故时间复杂度为 $O(n)$。

空间复杂度

• 需要额外 $O(h)$ 的空间作为系统栈空间，其中 $h$ 为树的最大高度。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int ans;

    int solve(TreeNode *rt, int d) {
        if (!rt) return 0;

        int tl = solve(rt->left, 0);
        int tr = solve(rt->right, 1);

        ans = max(ans, max(tl, tr));

        if (!d) return 1 + tr;
        return 1 + tl;
    }

    int longestZigZag(TreeNode* root) {
        solve(root, -1);
        return ans;
    }
};