题目描述

公司里有 n 名员工，每个员工的 ID 都是独一无二的，编号从 0 到 n - 1。公司的总负责人通过 headID 进行标识。

在 manager 数组中，每个员工都有一个直属负责人，其中 manager[i] 是第 i 名员工的直属负责人。对于总负责人，manager[headID] = -1。题目保证从属关系可以用树结构显示。

公司总负责人想要向公司所有员工通告一条紧急消息。他将会首先通知他的直属下属们，然后由这些下属通知他们的下属，直到所有的员工都得知这条紧急消息。

第 i 名员工需要 informTime[i] 分钟来通知它的所有直属下属（也就是说在 informTime[i] 分钟后，他的所有直属下属都可以开始传播这一消息）。

返回通知所有员工这一紧急消息所需要的 分钟数。

样例

输入：n = 1, headID = 0, manager = [-1], informTime = [0]
输出：0
解释：公司总负责人是该公司的唯一一名员工。

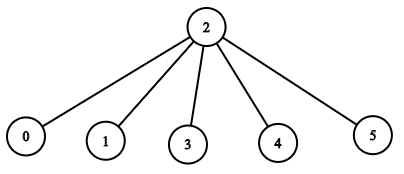
输入：n = 6, headID = 2, manager = [2,2,-1,2,2,2],
informTime = [0,0,1,0,0,0]
输出：1
解释：id = 2 的员工是公司的总负责人，也是其他所有员工的直属负责人，他需要 1 分钟来通知所有员工。
上图显示了公司员工的树结构。

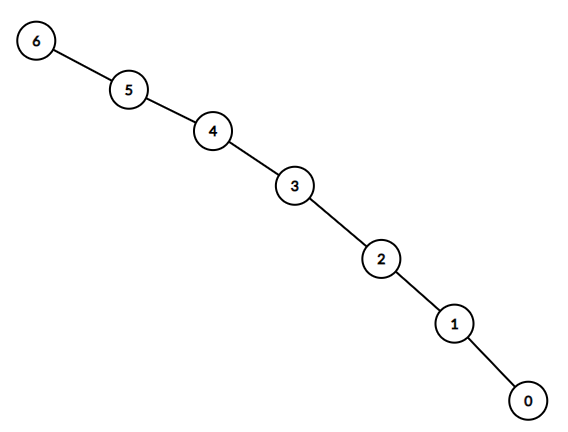
输入：n = 7, headID = 6, manager = [1,2,3,4,5,6,-1],
informTime = [0,6,5,4,3,2,1]
输出：21
解释：总负责人 id = 6。他将在 1 分钟内通知 id = 5 的员工。
id = 5 的员工将在 2 分钟内通知 id = 4 的员工。
id = 4 的员工将在 3 分钟内通知 id = 3 的员工。
id = 3 的员工将在 4 分钟内通知 id = 2 的员工。
id = 2 的员工将在 5 分钟内通知 id = 1 的员工。
id = 1 的员工将在 6 分钟内通知 id = 0 的员工。
所需时间 = 1 + 2 + 3 + 4 + 5 + 6 = 21。

输入：n = 15, headID = 0, manager = [-1,0,0,1,1,2,2,3,3,4,4,5,5,6,6],
informTime = [1,1,1,1,1,1,1,0,0,0,0,0,0,0,0]
输出：3
解释：第一分钟总负责人通知员工 1 和 2。
第二分钟他们将会通知员工 3, 4, 5 和 6。
第三分钟他们将会通知剩下的员工。

输入：n = 4, headID = 2, manager = [3,3,-1,2],
informTime = [0,0,162,914]
输出：1076

限制

• 1 <= n <= 10^5
• 0 <= headID < n
• manager.length == n
• 0 <= manager[i] < n
• manager[headID] == -1
• informTime.length == n
• 0 <= informTime[i] <= 1000
• 如果员工 i 没有下属，informTime[i] == 0。
• 题目 保证 所有员工都可以收到通知。

算法

(递归) $O(n)$

1. 预处理每个点的儿子结点的编号。此题相当于找从叶子结点到根结点的最长路。
2. 从根结点递归遍历。每层找到儿子结点最大的返回值，然后加上自己的通知时间，返回给上一层。

时间复杂度

• 每个点仅遍历一次，故时间复杂度为 $O(n)$。

空间复杂度

• 需要额外 $O(n)$ 的空间存储树型数据结构，以及递归时的系统栈空间。

C++ 代码

class Solution {
public:
    int solve(int rt, const vector<vector<int>>& ch, const vector<int>& informTime) {
        int tot = 0;
        for (int x : ch[rt])
            tot = max(tot, solve(x, ch, informTime));

        return tot + informTime[rt];
    }

    int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {
        vector<vector<int>> ch(n);
        for (int i = 0; i < n; i++)
            if (i != headID)
                ch[manager[i]].push_back(i);

        return solve(headID, ch, informTime);
    }
};