两种邻接表写法的差异
常见邻接表的两种写法:
一般图论问题的邻接表:
int h[N], e[M], w[M], ne[M], idx;
void add(int a, int b, int c) // 添加一条边a->b,边权为c
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
本题邻接表的写法:
vector<int> h[N];
本菜狗在昨天的比赛中误用了第一种,导致出错,o(╥﹏╥)o
先来一张图解释一下两种邻接表的差异:

为什么本题用第一种会错?
关键就在于遍历顺序
让我们再来读一下题:
题目
给定一棵 $n$ 个节点的树。
节点的编号为 $1∼n$,其中 1 号节点为根节点,每个节点的编号都大于其父节点的编号。
我们规定,当遍历(或回溯)到某一节点时,下一个遍历的目标应该是它的未经遍历的子节点中编号最小的那一个子节点。
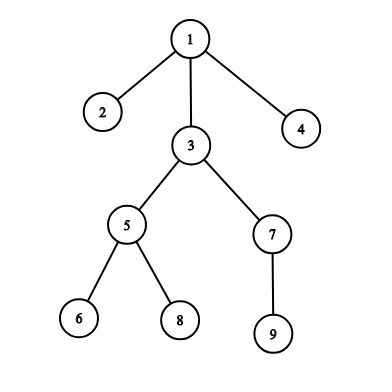
例如,上图实例中:
- 如果遍历根节点为 1 号节点的子树,则子树内各节点的遍历顺序为$ [1,2,3,5,6,8,7,9,4]$。
- 如果遍历根节点为 3 号节点的子树,则子树内各节点的遍历顺序为 $[3,5,6,8,7,9]$。
- 如果遍历根节点为 7 号节点的子树,则子树内各节点的遍历顺序为 $[7,9]$。
- 如果遍历根节点为 9 号节点的子树,则子树内各节点的遍历顺序为 $[9]$。
每个询问就是让你计算采用规定的 DFS 算法来遍历根节点为 $ui$ 的子树时,第 $ki$ 个被遍历到的节点的编号。
解析
题眼在于这句话:
我们规定,当遍历(或回溯)到某一节点时,下一个遍历的目标应该是它的未经遍历的子节点中编号最小的那一个子节点。
即题目是按照从小到大的方式插入点的,也希望我们从小到大遍历点
那么第一种邻接表就起不到这种效果
拿样例再举个例子:
写法一:
int h[N], e[M], ne[M], idx;
vector<int >q;
void add(int a, int b) // 添加一条边a->b
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u){
q.push_back(u);
for(int i = h[u]; ~i ; i = ne[i]) {
int j = e[i];
dfs(j);
}
}
遍历后得到的序列q为:
$[1, 4, 3, 7, 9, 5, 8, 6, 2 ]$
写法二:(本题正确写法)
vector<int>q;
//树的邻接表
vector<int> h[N];
void dfs(int u){
q.push_back(u);
for(int i = 0; h[u].size() ; i ++) {
dfs(h[u][i]);
}
}
遍历后得到的序列q为:
$ [1,2,3,5,6,8,7,9,4]$
如果没有顺序的要求,当然是两种都可以拉.゚ヽ(。◕‿◕。)ノ゚
本题还有一个坑就是:给点的时候是从2号点开始给,输入并没有根节点,一定要注意输入
避开上面两个坑就可以很容易ac了.゚ヽ(。◕‿◕。)ノ゚
本菜狗两个坑都没注意,所以没写出来,o(╥﹏╥)o
完结撒花.゚ヽ(。◕‿◕。)ノ゚


链式前向星。。。。
其实第一种写法每次在dfs之前把所有的子节点都存入vector之后在dfs也可以 不过时间效率有点低 但是还是ac啦
对,但这种方式不就是相当于开了n个vector,那么就等价于方法二了
不过最后我倒序插入了
我是用第一种写法的
倒序可以过吗?应该不行吧
但是我a了
求代码
中间有一段调试
谢大佬,学到了
不,您才是大佬
Orz
这都能找到你
看题解请移步其他大佬
谢谢你的分析,很清楚,我懂了
说到底还是太菜了不会用第二种方法
在写这道题之前我也一直以为存树的方法和存图的一样o(╥﹏╥)o
orz