$\color{green}{<–画图不易,点下这里赞一下吧}$
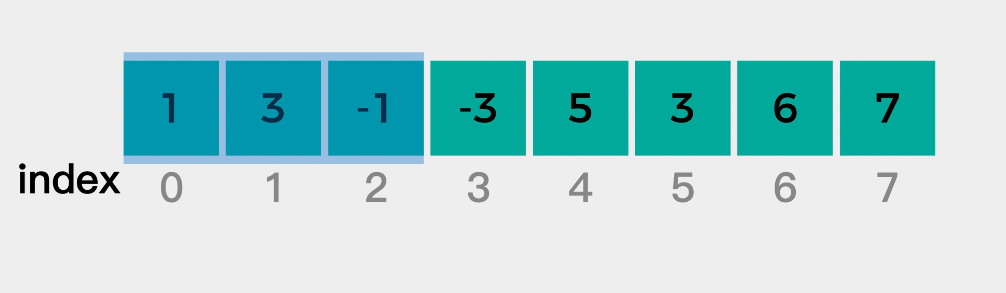
题目中提到了滑动窗口,我们先以示例为例看下什么是滑动窗口?在示例中,我们从数组中第一个元素开始遍历,由于窗口的大小是3,因此当遍历到第三个元素时,窗口就形成了。
 {:center}
{:center}
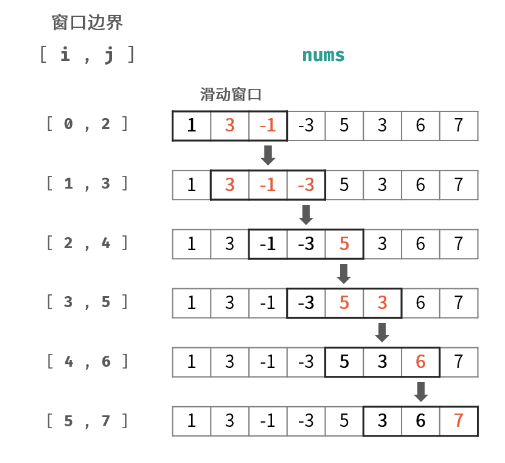
之后,继续遍历元素时,为了保持窗口的大小为3,左侧元素就需要从窗口中剔除。这样使得窗口一直在向右移动,直到考察到最后一个元素结束,这就是所谓的滑动窗口。
解题思路(以最大值为例):
由于我们需要求出的是滑动窗口的最大值。
-
如果当前的滑动窗口中有两个下标
i和j,其中i在j的左侧(i<j),并且i对应的元素不大于j对应的元素(nums[i]≤nums[j]),则:当滑动窗口向右移动时,只要
i还在窗口中,那么j一定也还在窗口中。这是由于i在j的左侧所保证的。因此,由于
nums[j]的存在,nums[i]一定不会是滑动窗口中的最大值了,我们可以将nums[i]永久地移除。 -
因此我们可以使用一个队列存储所有还没有被移除的下标。在队列中,这些下标按照从小到大的顺序被存储,并且它们在数组
nums中对应的值是严格单调递减的。 -
当滑动窗口向右移动时,我们需要把一个新的元素放入队列中。
为了保持队列的性质,我们会不断地将新的元素与队尾的元素相比较,如果新元素大于等于队尾元素,那么队尾的元素就可以被永久地移除,我们将其弹出队列。我们需要不断地进行此项操作,直到队列为空或者新的元素小于队尾的元素。
-
由于队列中下标对应的元素是严格单调递减的,因此此时队首下标对应的元素就是滑动窗口中的最大值。
-
窗口向右移动的时候。因此我们还需要不断从队首弹出元素保证队列中的所有元素都是窗口中的,因此当队头元素在窗口的左边的时候,弹出队头。
代码:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <deque>
using namespace std;
const int N = 1000010;
int a[N];
int main()
{
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; i ++ ) cin >> a[i];//读入数据
deque<int> q;
for(int i = 1; i <= n; i++)
{
while(q.size() && q.back() > a[i]) //新进入窗口的值小于队尾元素,则队尾出队列
q.pop_back();
q.push_back(a[i]);//将新进入的元素入队
if(i - k >= 1 && q.front() == a[i - k])//若队头是否滑出了窗口,队头出队
q.pop_front();
if(i >= k)//当窗口形成,输出队头对应的值
cout << q.front() <<" ";
}
q.clear();
cout << endl;
//最大值亦然
for(int i = 1; i <= n; i++)
{
while(q.size() && q.back() < a[i]) q.pop_back();
q.push_back(a[i]);
if(i - k >= 1 && a[i - k] == q.front()) q.pop_front();
if(i >= k) cout << q.front() << " ";
}
}


海绵宝宝你太强了
hhh,你的id我喜欢
林家傻儿狂吞114514个yxc,第二天,IOI炸了
把头像换掉,不然删你号
比y总代码清楚多了
关于为什么要使用单调队列的思考:
最直白的暴力算法为y总上课提及的O(nk)的方法在此不再赘述
那我们可能会想,如果用一个变量保存此时窗口的极值,当窗口滑动时只判断新加入的数与当前极值的关系不就可以了吗?
其实不然,因为当当前极值所在位置离开窗口时,我们并不知道剩下的数的大小关系,所以还需要重新比大小才能与下一个滑进来的数值比较。
因此,使用单调队列,排出大小关系,这样当极值滑出窗口时,我们能立刻确定出剩余数的极值,以便与新滑入的数进行比较。
谢谢大佬解惑
这里可以参考y总的代码,队列里面存元素下标而不是元素,因此判断是否出队就可以用
q.front() <= i-k来判断,如果是q.front() == a[i - k]难免存在特殊情况(队首元素刚好与a[i-k]相等但是此时的窗口起始位置并不位于i-k+1)导致错误可以举个例子吗。它的窗口起始位置不就是i-k的下标吗,它这里的i是从1开始的
q.push_back(a[i])他是将元素入队,而不是元素的下标。数组不保证每个位置的元素都是不一样的,但是每个位置下标是肯定不同的啊,所以q.front() == a[i - k]如果数据稍微脏一点就可能有问题吧,比如某个下标x的数据a[x]和a[i - k]正好一样但是x > i - k,x正好位于队尾的时候就有可能被错误地出队了。我理解你说的这种情况了,但是实际上不会出现。
因为首先它写的是q.pop_front(),而且它的queue的长度是时刻大于等于1的,说明其中至少有两个元素。q.front() == a[i - k]。 你想说的a[x] 应该就是q.front(), q.front()这个元素的下标应该是 deque 里面下标最小的, 所以实际上不可能出现 x > i - k, 换句话说x不可能位于队尾,所以哪怕a[x]和a[i - k], 赶出去的也是min(x,i-k)下标中更小的那个, 而且它用的也是q.pop_front(),保证一定是前面的先走。
我试了一下数据 1 1 1 2 2 2 3 3, 它的结果也是正确的
“为了保持队列的性质,我们会不断地将新的元素与队尾的元素相比较,如果新元素大于等于队尾元素,那么队尾的元素就可以被永久地移除,我们将其弹出队列”,可是代码里面为啥是 q.back() < a[i],而不是q.back() <= a[i]呢?
我的代码入队时用的数组元素,因此相等元素的要保留在队列里。所以不带等号。
如果入队的数组下标,则不用保留。所以带等号。
这里为什么一定不能加等号呢,我加了等号就错了
相等的删了有什么关系吗,不能理解
一样的疑问
如果把相等的弹出,if(i - k >= 1 && q.front() == a[i - k])这个判断可能将会成立,导致队列清空!!!!
eg:输入数据:5 2
3 3 3 3 3
不得不说,代码有些地方很强
在下面弹出元素 if(i-k >=1 && q.front()==a[i-k] )的时候,如果入队用的数组元素,无法确定当前队头是后插入的还是原来应该弹出的那个,会误把后插入的那个给弹出;而如果入队的是数组下标则没这个问题,这样即使两个相同值的元素也能进行区分。
新元素进来,重复的元素要么全被干掉,要么全被保留。考虑是否有漏弹、误弹现象只需要考虑重复元素被保留的情况。到了弹出的时刻,因为队列中元素由老到少排队,队头是资历最老的(最先进来的)。于是重复元素会被按序弹出。
while(q.size() && q.back() > a[i]) //新进入窗口的值小于队尾元素,则队尾出队列
q.pop_back(); 我套用你的例子,发现在这一步就已经队列清空了。
图借走了海绵宝宝
为啥判断是否为队头的时候是i-k啊,i为右端点的话,左端点不应该是i-k+1吗
大佬
这里是从下标1开始的哦
就算下标是1 也应该是i - k + 1才能找到左端点把
队头等于i-k对应的元素说明队头该出队了,因为i在变,i变了i-k也变了,i-k+1是队头,i++之后i-k就是队头,所以队头出队
这里的i是窗口右端点右边的第一个数,并不是右端点。
不是我问的
请问q.fornt()==a[i-k]是啥意思?
是不是满足这个if句子之后就表示现在的窗口大于题目要求的k窗口大小 从而导致pop.fornt呢?
就是说队头是最大的,队头如果在窗口内的时候我们就输出队头,而一旦队头滑出了窗口,我们就要将队头从队里移动出去,q.fornt()==a[i-k]判断的就是滑出去的是不是队头
为什么还要判断滑出去的是不是队头,窗口不断向右移动,滑出去的不应该一定是队头吗?
因为窗口已经向右移动了,如果之前的队头没有在前面的比较操作中被删除,那么这次就要把它删除,保证窗口内成员个数为k
您好,代码中
if(i - k >= 1 && q.front() == a[i - k])//若队头是否滑出了窗口,队头出队
该判断队头是否滑出滑动窗口,直接通过值比较而不是通过索引比较,可能会存在特殊情况,导致误判吧?
看起来是的,可以hack一下
我也觉得
对单调栈和单调队列还不懂的朋友们可以看看这篇博客,感觉还是挺详细的:https://raelum.blog.csdn.net/article/details/128969669
作者大大(^_^)
while(q.size() && q.back() > a[i]) //新进入窗口的值大于队尾元素,则队尾出队列
这里是不是注释写反了呀,而且上面这个好像是求最小值的吧
下面那个求最大?
你说的对,已给正,谢谢
想问下大佬们,while(q.size() && q.back() > a[i]) 这块q.back() >= a[i]为什么不行
同问
太强了,y总的代码死活看不明白,一看你的就懂了,orz
佬 如果没有你还有你的图解 我该怎么办呀(哭
写的太好了,悟了,顶上去
###Orz O zrO
$$\large \color{red}ORZ$$
借鉴一下作者的笔记记录在博客方便复习,谢谢佬
#include[HTML_REMOVED]
using namespace std;
const int N=1e6+10;
int a[N],stk[N],st[N];
int main()
{
int n,k; cin>>n>>k;
} //有没有大神能告诉我我哪儿错了