题目描述

Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.

In one shift operation:

• Element at grid[i][j] moves to grid[i][j + 1].
• Element at grid[i][n - 1] moves to grid[i + 1][0].
• Element at grid[m - 1][n - 1] moves to grid[0][0].

Return the 2D grid after applying shift operation k times.

Example 1:

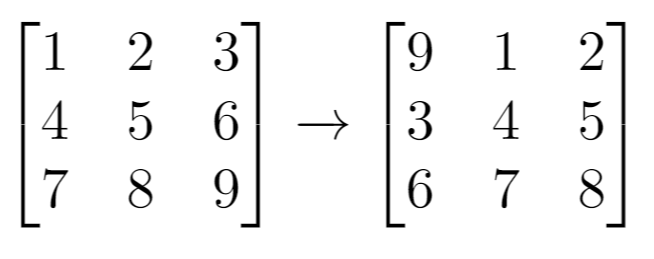
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:

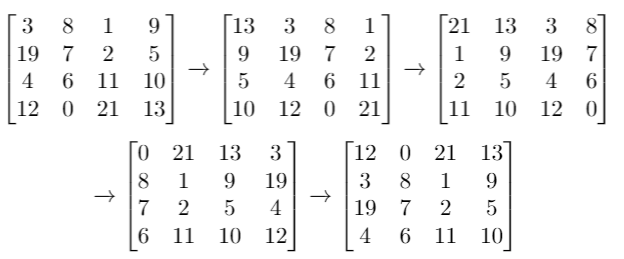
Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m <= 50
• 1 <= n <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

题意：给你一个 m 行 n列的二维网格grid和一个整数k。你需要将grid 迁移 k次。

每次「迁移」操作将会引发下述活动：

位于 grid[i][j]的元素将会移动到grid[i][j + 1]。
位于 grid[i][n - 1]的元素将会移动到 grid[i + 1][0]。
位于 grid[m - 1][n - 1]的元素将会移动到 grid[0][0]。
请你返回k次迁移操作后最终得到的 二维网格。

算法1

(取模) $O(nm)$

题解：我们的确可以使用模拟的做法来完成这道题，那么时间复杂度将是$O(nmk)$。接下来我们考虑更简单的做法，我们考虑每一个元素在移动$k$次之后的最终位置，对于纵坐标，每次移动都会向右移动，所以最终的纵坐标就是new_col = (old_col + k) % m。对于横坐标，我们知道在移动$m$次之后才会向下移动一格，如果k + old_row < m，说明最终还在同一行，否则我们计算k - (m - 1 - old_col)代表从下一行第一个位置开始还需要移动多少步，除以m加上1就是行的变化次数。

    vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<int>> res(n,vector<int>(m));
        for(int i = 0 ; i < n ; i ++)
        {
            for(int j = 0 ; j < m ; j ++)
            {
                int new_col = (j + k) % m;
                int step = (k - (m - 1 - j)),row_gap;
                if(step <= 0) row_gap = 0;
                else if(step % m == 0) row_gap = step / m;
                else row_gap = step / m + 1;
                int new_row = (i + row_gap) % n;
                res[new_row][new_col] = grid[i][j];
            }
        }
        return res;
    }