算法提高课汇总

理解题意

题目求带权树上的最长路径, 也可称为树的直径. 关键是找到一种快速枚举树上
所有路径的方法.

$DP$分析

状态表示 $dp(u)$

• 集合: 任意以一点作为树根后, 树节点相对根就有了高低之分. $dp(u)$表示最高节点为$u$的
  所有路径集合.

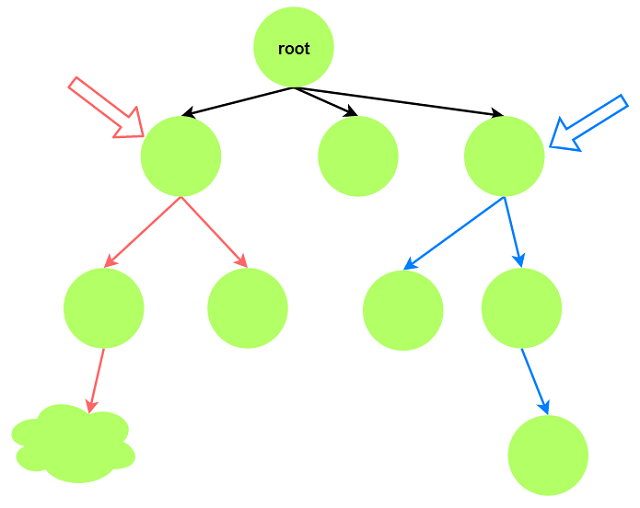
• 属性: Max路径长度的最大值.

状态计算

为保证当前节点$u$是路径最高点, 向下枚举以子节点为根到叶节点的最长路径.

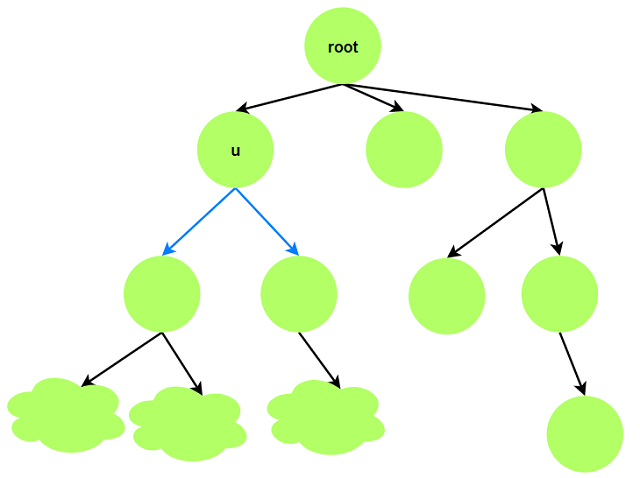
$dp(u)$即所有其子节点向下的路径的最长与次长值之和, 若路径值为负数可以忽略.

具体实现

在确定根后, 树的边应该为有向边. 为防止节点“回头”向上搜索, 在$dfs$过程中加入参数$father$ —
当前节点的父节点.

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 10010, M = 2 * N; //无向边

int n;
int h[N], e[M], w[M], ne[M], idx;
int ans; //每次枚举就能得到dp(u), 顺序自底向上, 可以不存储dp(u)

void add(int u, int v, int c)
{
    e[idx] = v, w[idx] = c, ne[idx] = h[u], h[u] = idx ++ ;
}

int dfs(int u, int father)
{
    int d1 = 0, d2 = 0; //u->子节点->根 的最长路径的最大与次大值 负数可忽略所以初值为0
    for ( int i = h[u]; ~i; i = ne[i] )
    {
        int v = e[i];
        if ( v == father )  continue; //防止向上搜索
        int d = dfs(v, u) + w[i];
        if ( d >= d1 )  d2 = d1, d1 = d;
        else if ( d > d2 )  d2 = d;
    }
    ans = max(ans, d1 + d2);
    return d1; //返回从u到根的最大值
}

int main()
{
    cin >> n;
    memset(h, -1, sizeof h);
    for ( int i = 1; i < n; i ++ )
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }

    dfs(1, -1);
    cout << ans << endl;

    return 0;
}

无权树的直径求解

对于无权树(可认为边权均为1), 可以按如下方法求数的直径:

1. 取任意一点$a$为起点, 找到距离$a$最远的一点$u$.

2. 找距离$u$最远的节点$v$.

$u\rightarrow v$的路径即为树的一条直径.

证明: 若$u\rightarrow v$不是树的一条直径, 即$u$不是一条直径直径的端点.
假设树中直径为$c\rightarrow d$, 与$a\rightarrow u$存在两者关系.

1. 二者无交点

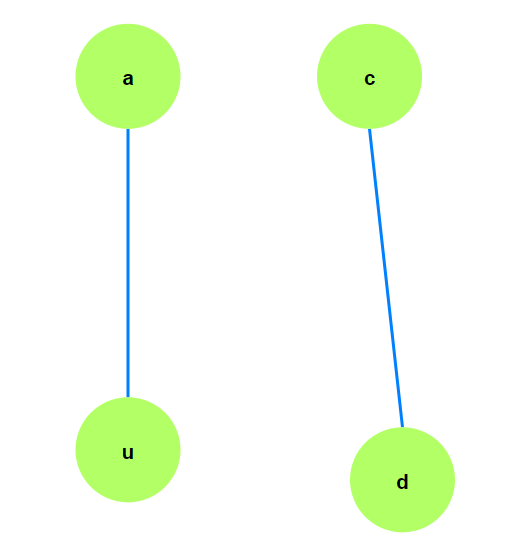
树上任意两点联通, 所以从$a$存在一条到$d$的路径.

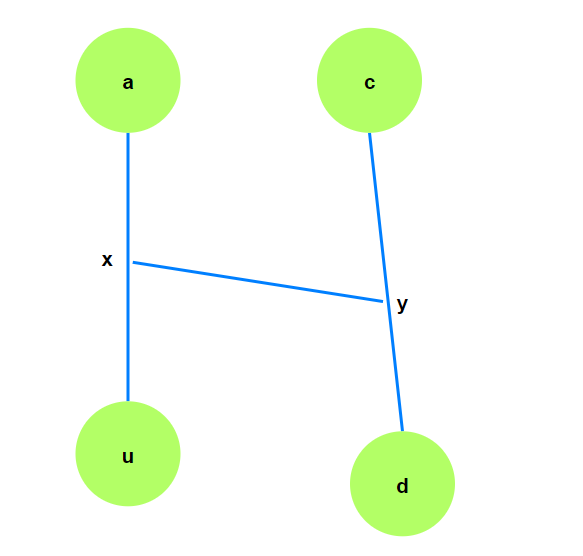
由于距离$a$最远的顶点是$u$, 所以$[a, x] + [x, u]\ge [a, x] + [x, y] + [y, d]$ -->
$[x, u]\ge [x, y] + [y, d]$ --> $[x, u] + [x, y]\ge [y, d]$ --> $[x, y] + [x, y] + [y, c]\ge [y, d] + [y, c]$
由于$[y, d] + [y, c]$即树的直径$c\rightarrow d$, 所以从$u$到$c$也是直径. 即$u$作为直径的一个端点.

2. 二者相交

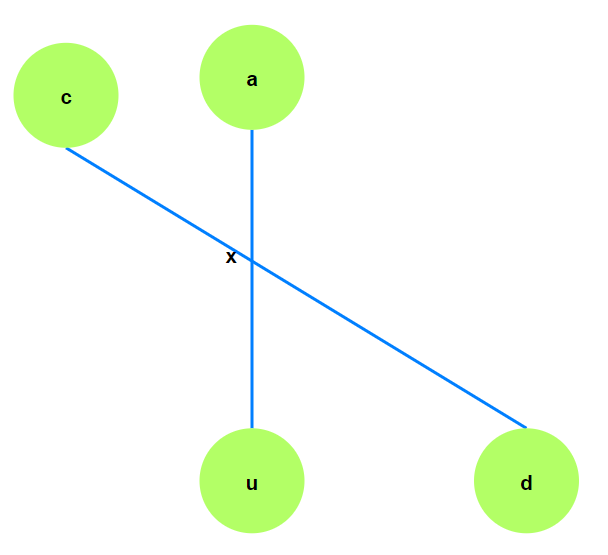
可以认为$x\rightarrow y$退化为一个点. 可以用类似的方式证明.