算法提高课汇总

$IDA^*$

在迭代加深中, 若搜索深度超过当前最大深度$depth$, 则直接返回.

$IDA^*$中使用估价函数 — 计算当前状态$u$到最终解至少还要走多少步$f(u)$. 若
当前深度$d + f(u)\gt depth$, 可以直接返回.

$f(u)$的限制: 不超过真实步数即可.

算法思路

时间估计

若抽取长度为$i$, 则共有$n - i + 1$段. 对于每一段, 剩余书有$n - i$个, 有$n - i + 1$空格, 除去
自身所在空格, 则有$n - i$个空格可选, 即有$n - i$个选择. 则所有方案有$\sum_{i = 1}^{14} (n - i + 1)\times (n - i)$

观察每次移动结果: 将绿色段移动至箭头所指节点的后面:

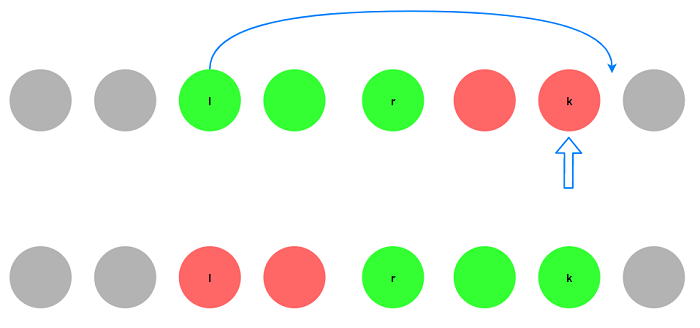
相当于将$(l, r)$与$(r + 1, k)$两段交换位置, 可以只保留一种交换方式(比如从前段向后段交换),
所以每种等效方案计算了两次, 因此方案数为$(15\times 14 + 14\times 13 + … + 2\times 1)/2 = 560$.

题目限制搜素最深有4层, 所以时间复杂度最坏为$O(560^4)$. 考虑用$IDA^*$优化.

估价函数

考虑每个元素的后继: 对于正确序列$1, 2, …, n$, 每个元素$x[i]$与其后继的关系是$x[i] + 1 == x[i + 1]$.

观察每次交换的结果: 一次交换最多改变3个元素的后继:

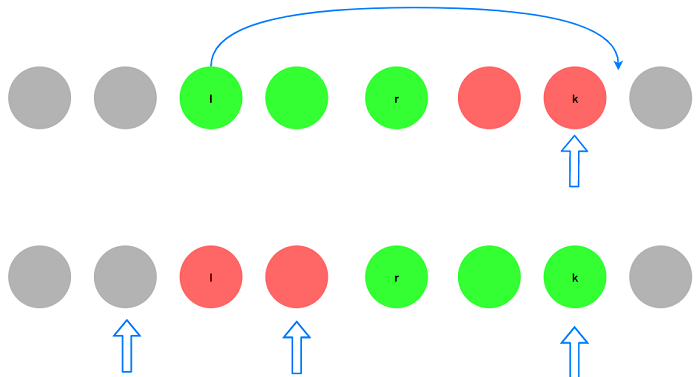
最好的情况是每次改变的3个后继从错误后继转为正确后继. 假设当前状态错误后继的个数为$tot$,
每次最多修改3个, 所以从当前状态到最优状态至少需要$\lceil tot/3\rceil = \lfloor (tot + 2)/3\rfloor$步.

代码实现

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 15;

int n;
int q[N];
int w[5][N]; //存储每层对应的现场

int f()
{//估价函数
    int tot = 0;
    for ( int i = 0; i + 1 < n; i ++ )
        if ( q[i] + 1 != q[i + 1] )
            tot ++ ;
    return (tot + 2) / 3;
}

bool dfs(int u, int depth)
{
    if ( u + f() > depth )  return false;
    if ( f() == 0 )     return true; //没有错误后继 说明找到最优解

    for ( int len = 1; len < n; len ++ ) //枚举长度
        for ( int l = 0; l + len - 1 < n; l ++ )
        {
            int r = l + len - 1; //[l, r]
            for ( int k = r + 1; k < n; k ++ ) //交换到k之后 可以之和后段交换 避免重复
            {
                memcpy(w[u], q, sizeof q); //保存现场
                int x, y = l; //将[l, r]与[r + 1, k]交换
                for ( x = r + 1; x <= k; x ++, y ++ ) q[y] = w[u][x];
                for ( x = l; x <= r; x ++, y ++ )     q[y] = w[u][x];
                if ( dfs(u + 1, depth) )    return true;
                memcpy(q, w[u], sizeof q); //恢复现场
            }
        }
    return false;
}

int main()
{
    int T;
    cin >> T;
    while ( T -- )
    {
        cin >> n;
        for ( int i = 0; i < n; i ++ )  cin >> q[i];

        int depth = 0;
        while ( depth < 5 && !dfs(0, depth) )   depth ++;

        if ( depth < 5 )    cout << depth << endl;
        else    puts("5 or more");
    }
    return 0;
}