算法三

背包(本质：组合问题求最优解) + 贪心(只取余数前3大即可) O(3k * 4 * k) （贪心优化后第一维从n降到3k，完美）

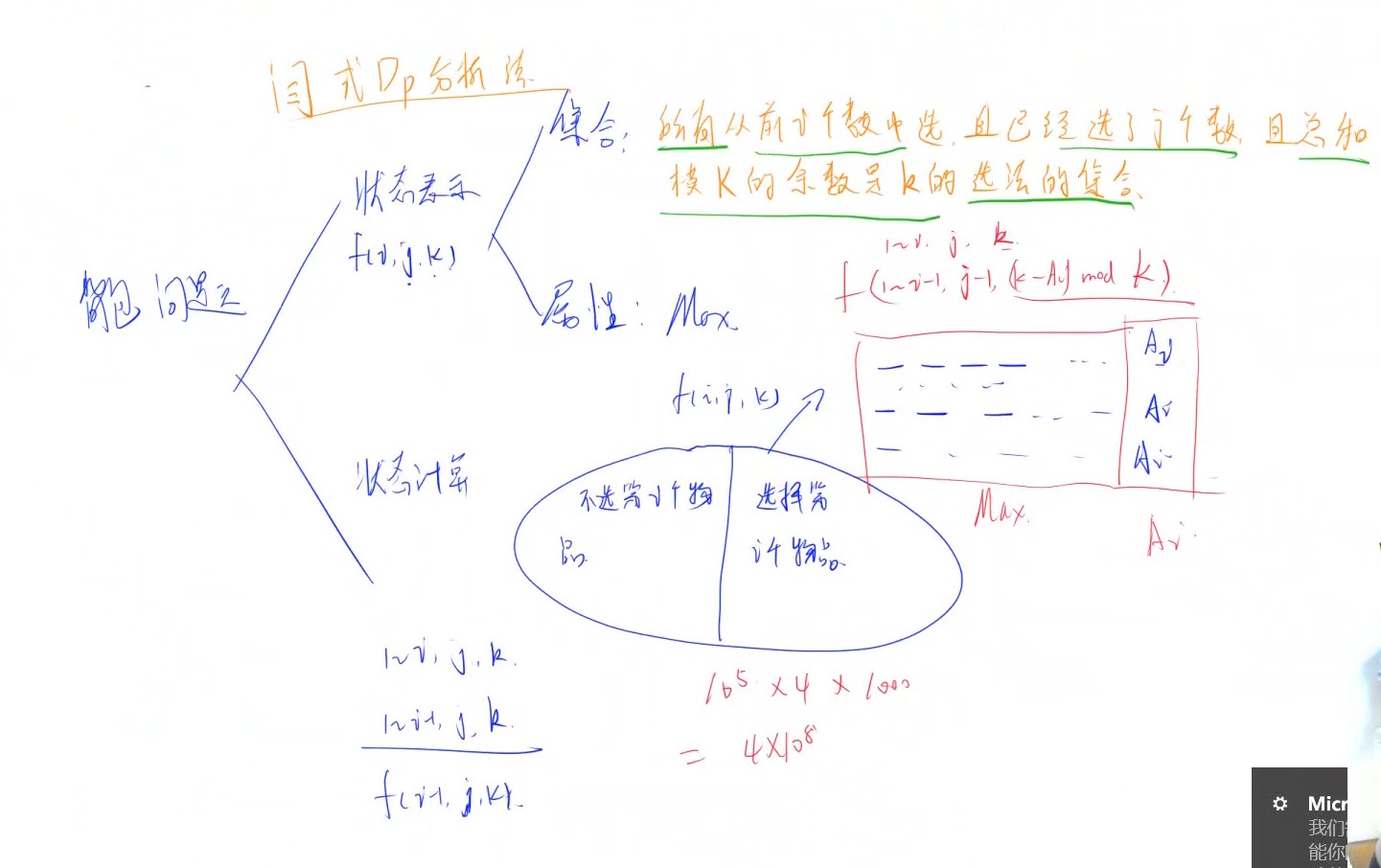
• 状态表示
  • 集合：f[i][j][k] : 所有从前i个数中选，且已经选了j个数， 且总和模K的余数是k的选法集合（每一维都是一个限制），答案就是f[n][3][0],背包问题空间优化
  • 属性： Max
• 状态计算
  • 不选第i个物品 f[i-1][j][k]
  • 选择第i个物品 f[i-1][j-1][(k - x % m + m) % m] // C ++ 正数模

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 1010;

int n,m;
vector<int> a[N];
int f[4][N]; // 背包问题空间优化

int main()
{
    scanf("%d%d",&n, &m);

    for(int i=0;i<n;i++)
    {
        int x;
        scanf("%d",&x);
        a[x % m].push_back(x);
    }

    memset(f,-0x3f,sizeof f);
    f[0][0]=0;

    for(int i=0;i<m;i++)
    {
        sort(a[i].begin(),a[i].end());
        reverse(a[i].begin(),a[i].end());

        for(int u=0;u<3 && a[i].size(); u ++ ) // 贪心，只取前3大数即可
        {
            int x=a[i][u];

            for(int j=3;j>=1;j--) // 背包问题空间优化，j从大到小循环
                for(int k=0;k<m;k++)
                    f[j][k] = max(f[j][k], f[j-1][(k - x % m + m) % m] + x);

        }
    }

    printf("%d\n",f[3][0]);

    return 0;
}

算法1

(暴力三重循环) $O(n^3)$ 过 6/11个数据

#include <iostream>
#include <cstdio>

using namespace std;


const int N = 1e5 + 10;

int n,K;
int a[N];

int main()
{
    scanf("%d%d",&n,&K);

    for(int i=0;i<n;i++) scanf("%d",&a[i]);

    int res=0;
    for(int i=0;i<n;i++)
    {
         for(int j=i+1;j<n;j++)
        {
            for(int k=j+1;k<n;k++)
            {
                int t=a[i]+a[j]+a[k];
                if(t % K == 0)
                    res=max(res,t);

            }
        }
    }

    printf("%d",res);

    return 0;

}

算法2

(取模优化，枚举前两个余数，确定第三个余数) $O(K^2)$

参考文献

一花一世界

C++ 代码

#include <cstdio>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 1010;

int n,K;
vector<int> a[N];

int main()
{
    scanf("%d%d",&n,&K);

    for(int i=0;i<n;i++)
    {
        int x;
        scanf("%d",&x);
        a[x % K].push_back(x);
    }

    for(int i=0;i<K;i++) sort(a[i].begin(),a[i].end()), reverse(a[i].begin(),a[i].end()); // 从大到小排序

    int res=0;
    for(int i=0;i<K;i++)
        for(int j=0;j<K;j++)
        {
            //int t= = K - (i + j) % K ; // 这样写是错误的!  C++中转化为 正余数 下面这样 再加再%
            int t = (K - (i + j) % K + K) % K ; // 思路：确定两个余数，枚举第三个余数,时间复杂度O(K^2 ~ 10^6)
            if(a[i].size() && a[j].size() && a[t].size()) // 余数对应的数存在,才讨论接下来的情况
            { 
                int b = *(a[i].begin()), c, d; // 取余数对应的最大数
                if(i != j && j != t && i != t) // 1.三个余数都不相同
                {
                    c = *(a[j].begin()), d = *(a[t].begin());
                }
                else if(i == j && i != t) // 2.有两个余数相等
                {
                    if(a[i].size() < 2) continue; // 数不能重复

                    c = *(a[j].begin() + 1); // 取第二大的数
                    d = *(a[t].begin());
                }
                else if(i == t && i != j ) 
                {
                    if(a[i].size() < 2) continue; 

                    c = *(a[j].begin()); 
                    d = *(a[t].begin() + 1);
                }
                else if(j == t && i != t)
                {
                    if(a[j].size() < 2) continue;

                    c = * (a[j].begin());
                    d = * (a[j].begin() + 1);
                }
                else  // 3.三个余数都相等
                {
                    c = *(a[i].begin() + 1);
                    d = *(a[i].begin() + 2);
                }

                res=max(res,b+c+d);
            }


        }


    printf("%d\n",res);

    return 0;


}