算法提高课汇总

迭代加深

what

一般的$dfs$每次从一个分支一路向深处走直到遇到叶节点返回. 若问题搜索树中错误❌分支的深度较深,
而正确答案实际上在很浅的位置时, 会白白损耗很多时间.

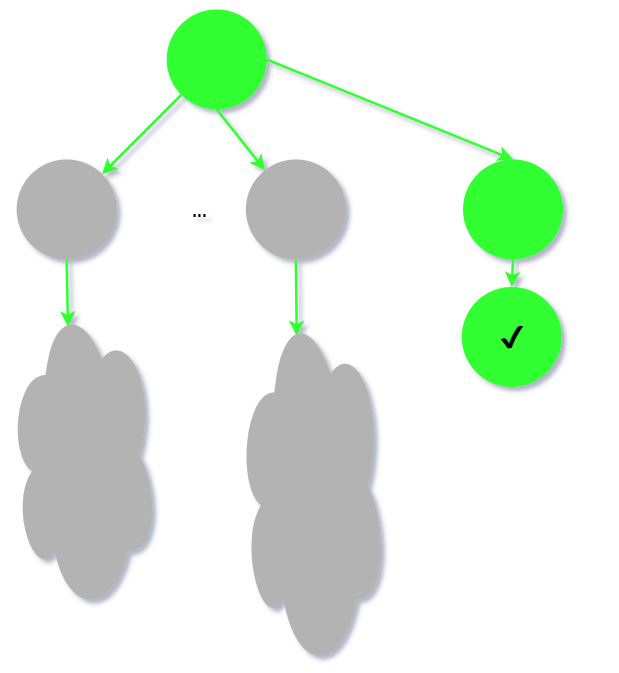
迭代加深的思想是每次限定一个最大搜索深度, 若超过则直接返回. 深度迭代增加, 直到当前深度下
找到了正确✔答案.

也就是迭代扩大搜索范围, 用限制深度的方式避免无谓的向下搜索.

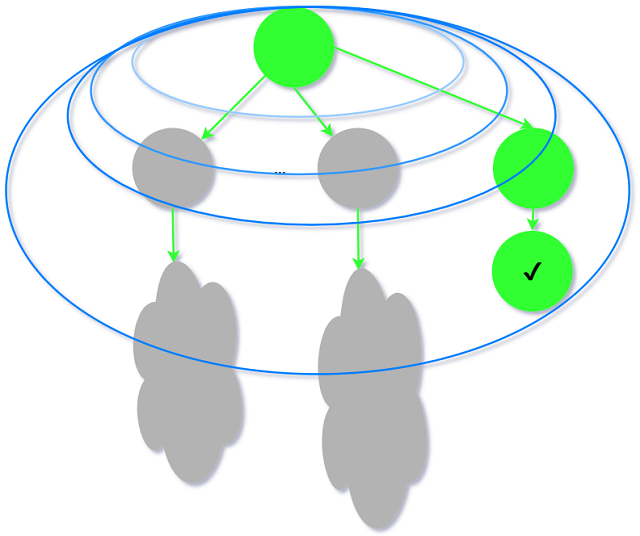
是否得不偿失

虽然我们防止进入深层的错误节点, 但同时我们多次重复遍历了浅层的节点. 但一般来说, 浅层
次的重复相比深层节点数目是可以忽略的.

例如设$dfs$每个节点都有$k$个分支, 则第$n$的节点个数为$k^n$, 而$1\sim n - 1$层节点数
的和为(重复的节点)$1 + k + k^2 + … + k^{n - 1} = \frac{k^n - 1}{k - 1}$.

与$bfs$对比

迭代加深好像类似$bfs$ — 按层的方式搜索, 实际两者大相径庭:

• $bfs$每次将某层节点全部加入, 空间复杂度为指数级; 而迭代加深仍是$dfs$, 空间复杂度为$O(depth)$.

• 迭代加深可以与$A^*$配合使用.

算法思路

$N$最大为100, 搜索路径最深情况: 每次向前增加1, 则最深可能有100层.

而如果采用$1, 2, 4, …, $可以在接近$\lg(N)$的深度得到答案.

为防止在错误路径中搜索过深, 可以使用迭代加深算法.

搜索顺序

按序列下标顺序搜索每个元素的数值.

剪枝优化

• 优化搜索顺序: 搜索某个元素的数值时, 从大到小枚举所有可能.

• 删除等效冗余: 当前元素值为之前序列的2个数字之和, 可能不同组合之和相同.
  可以在每层加入标记数组以防止重复搜索.

具体代码

#include <iostream>

using namespace std;

const int N = 110;

int n;
int path[N];

bool dfs(int u, int depth)
{
    if (u > depth)  return false; //超出限制
    if (path[u - 1] == n)   return true; //得到n

    bool st[N] = {0}; //判重 -- 排除等效冗余
    for ( int i = u - 1; i >= 0; i -- )
        for ( int j = i; j >= 0; j -- )
        {//从大到小枚举 -- 优化搜索顺序
            int s = path[i] + path[j];
            if (s <= path[u - 1] || s > n || st[s])  continue;

            st[s] = true; //不属于现场 每层独立 
            path[u] = s; //由于每次覆盖原值  可以不显式恢复现场
            if (dfs(u + 1, depth))  return true;
        }
    return false;
}

int main()
{
    path[0] = 1;
    while (cin >> n, n)
    {
        int depth = 1; //最大深度
        while ( !dfs(1, depth) )    depth ++ ; //“迭代”
        for ( int i = 0; i < depth; i ++ )  cout << path[i] << ' ';
        cout << endl;
    }
    return 0;
}