参考文献

解析：

本题直接从坐标角度考虑是比较复杂的，转化为用区间考虑！

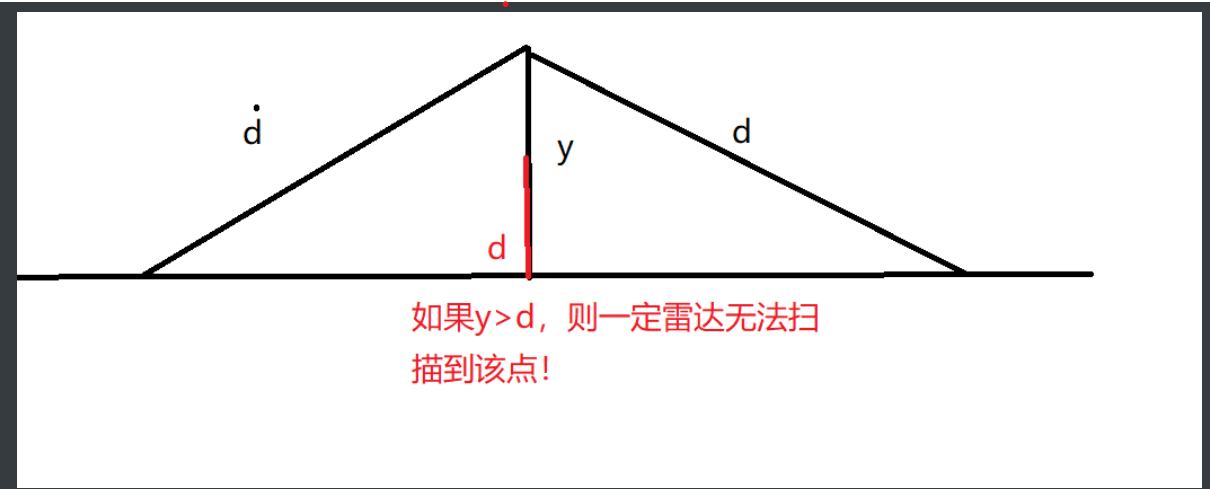
对于每个岛的xy来说，如果y>d，那么雷达一定扫描不到该岛！(垂线段最短！)

对于每个点来说，如果雷达要想扫描到该点，必须再该点的(x-len,x+len)范围内，len=sqrt(y^2-d^2);

因此，每个点都可以转化为一个区间。

所以，问题就变成了如何只用一个点去覆盖尽可能多的区间从而使得雷达的使用量最小。

贪心的策略为：

1 将区间按照右端点排序，如果右端点没能比下一个点的左端点大，也就是这个点无法在下一个区间内，那么就说明这个雷达无法同时涵盖多个区间，这时候cnt++,并且更新右端点为当前无法覆盖区间的右端点，将其设置为新的雷达。

2 如果可以包括，就continue；

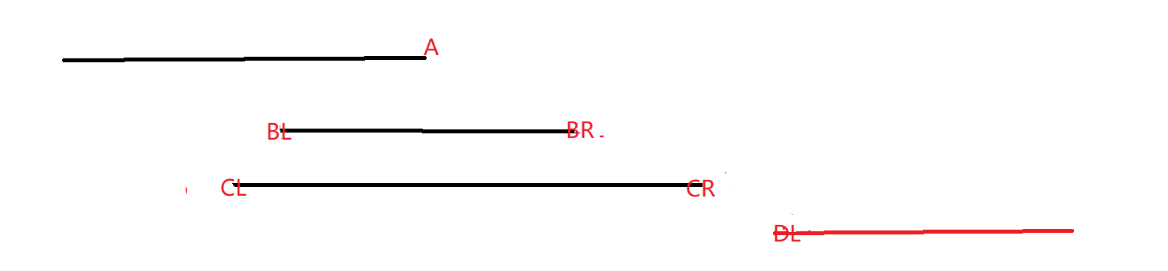
ex.下图一开始选择A为起始点，A先跟BR比较，比较后A>BR不跟新，跳过，再跟C比较CL<A,跳过，跟D比较，

A<DL，更新雷达为DL。

C++ 代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=1010;
struct segment{
    double l,r;
    //要对区间进行排序，所以重载运算符 
    bool  operator<(const segment &t)const{
        return r<t.r;
    }
}seg[N];
int x[N];
int y[N];
int main()
{
    int n,d;
    bool failed=false ;
    scanf("%d%d",&n,&d);
    for(int i=0;i<n;i++){
        scanf("%d%d",&x[i],&y[i]);
        if(y[i]>d) failed=true; 
    }
    if(failed) printf("-1");
    else {
        for(int i=0;i<n;i++){
            double len=sqrt(d*d-y[i]*y[i]);
            seg[i].l=x[i]-len;
            seg[i].r=x[i]+len;
        }
        sort(seg,seg+n);
        int cnt=1;
        double first =seg[0].r;
        for(int i=1;i<n;i++){
            if(first>=seg[i].l)continue;
            else {
                cnt++;
                first=seg[i].r;
            }
        }
         printf("%d",cnt);
    }

    return 0;
}