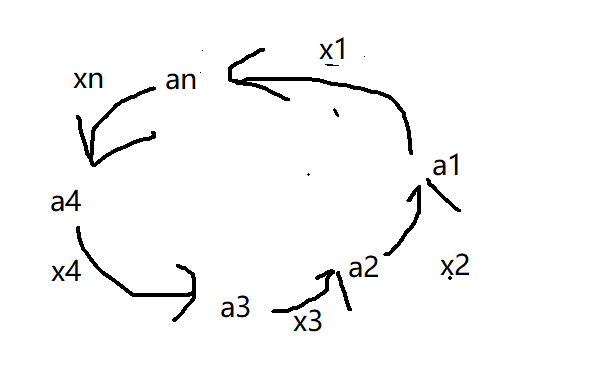
说明：

其中x为传递糖果所需要用的代价数，

若x>0，则说明传递的方向是从ai->a[i-1];

若x<0,那么传递的方向是从a[i-1]>ai;

分析题目：目标+限制

目标：要使得代价和最小。

也就是使得|x1|+|x2|+…|xn|最小

限制：使得a[i]=ave(a);//ave(a)也就是平均值

这是一个多元代数式，求最小值，应该想办法转化为1元代数式。

我们尝试找出关系式：

对于每个a[i]:

_a表示a的平均值

a[1]-_a=x2-x1

a[2]-_a=x3-x2

....

a[n-2]-_a=x[n-1]-x[n-2]

a[n-1]-_a=x[n]-x[n-1]

a[n]-_a=x[1]-x[n]

整理为a一边，x一边：

x[n]=x[1]+_a-a[n];

x[n-1]=x[n]+_a-a[n-1]

带入x[n]：其实尾部两式直接相加即可得到x[n-1]

x[n-1]-x1=2_a-a[n]-a[n-1];

x[n-2]=x[n-1]-x[n-2]+_a;

尾部三式相加整理：

x(n-2)-x1=3_a-a[n]-a[n-1]-a[n-2];

又上面式子：

x[n]=x[1]+（_a-a[n]）;

x[n-1]=x[1]+（2_a-a[n]-a[n-1]）;

x(n-2)=x[1]+（3_a-a[n]-a[n-1]-a[n-2]）;

…

xi=x[1]+【(n+1-i)_a-a[n]-a[n-1]-a[n-2]-…a[i]】;

特别的：

当i=1时候：

由于n_a=(a[1]+a[2]+..a[n])

所以：x[1]=x[1]+0;

可以总结每一项都可以由x1表示

而且可以转化为xi=x1+ci的形式：

又c[n]=_a - a[n]

c[n-1]=2_a - a[n]-a[n-1]

c[n-2]=3_a - a[n]- a[n-1] -a[n-2]

所以：会发现每一项都比前一项多了一个_a再多减去一个a[n]

c[i]=c[i+1]+_a-a[i];

注意c[1]=0;(x1=x1+0)

从而将|x1|+|x2|+|x3|+…|xn|的最小化问题转化为|x1+c1|+|x1+c2|+......|x1+cn|的坐标模型：

也就是坐标轴上的点

c1,c2,c3......cn到x1的最小值：

而由几何意义不难想到:

x1在中位数的时候取得最小值：

即x1=c[i+1/2];(i从1开始，如果i从0开始，x1=c[n/2])；

C++ 代码

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1000010;
typedef long long LL;
int n;
int a[N];
LL c[N];
int main()
{

scanf("%d",&n);
LL sum=0;
for(int i=1;i<=n;i++) {
    scanf("%d",&a[i]);
}
for(int i=1;i<=n;i++){
    sum+=a[i];
}
LL ave=sum/n;
for(int i=n;i>1;i--){
    c[i]=c[i+1]+ave-a[i];
}
c[1]=0;
sort(c+1,c+n+1);
LL res=0;

for(int i=1;i<=n;i++){
    res+=abs(c[i]-c[(n+1)/2]);
}
printf("%lld\n",res);
    return 0;
}