算法提高课汇总

算法思路

搜索顺序

枚举原木棒的长度($length = maxv\sim sum$, 其中$maxv$为断木棍最大长度, $sum$为所有断木棍长度之和),
对于每个原木棒长度$length$, 枚举每个断木棍拼接方案(和哪几个其他木棍拼接).

剪枝优化

1. 可行性剪枝

1. 拼接完成后所有木棒的长度之和等于$sum$, 可以只枚举满足$sum\;\%\;length == 0$的length值.
2. 在拼接某个原木棒时, 新加入断木棍后长度之和需要$\le length$.

2. 优化搜索顺序

拼接原木棒时, 优先考虑长度长的断木棍, 其分支数目更少.

3. 删除等效冗余

1. 拼接某个原木棒时, 需要考虑的是断木棍的长度和是否等于$length$, 而不用考虑断木棍的顺序.
   即是组合问题而不是排列问题. 具体表现在代码上: $dfs$函数参数start — 拼接当前原木棒
   可以从下标为start的断木棍开始考虑.

2. 拼接某个原木棒时, 若选择当前断木棍最终无合法方案(无解), 则我们可以跳过后续与其长度相同
   的断木棍(由优化搜索顺序, 我们是按长度降序的顺序考虑断木棍的).

   一种直观理解: 长度相同的断木棍本质上没区别.
   反证法: 若当前木棒继续考虑与当前长度为$l$断木棍相同长度的后续木棍, 最终找到合法方案.
   我们可以将当前木棍与替换木棍交换位置, 对最终解没有影响.(只需要考虑长度)
   此时选择当前断木棍又有解, 矛盾.

3. 拼接某个原木棍时, 若当前断木棍是第一个加入拼接的木棍, 考虑加入后续所有木棍最终发现无解,
   则可以直接返回.

   一种直观理解: 给你这么多选择你都不中用, 后续选择更少你也没希望了.
   反证法: 假设此时不考虑第一个加入拼接的断木棍$x$, 考虑其他木棍最后找到一个合法方案.
   也就是最终$x$找到了其归宿 — 拼接为某个原木棒. 由于拼接顺序任意, 可以将$x$替换成
   其原木棍第一个加入拼接的木棒. 也就是说$x$作为第一个加入拼接的木棒是可以有解的, 矛盾.

4. 拼接某个原木棒时, 若当前断木棍是最后一个加入拼接的木棍(也就是当前木棍已拼接完毕),
   考虑后续断木棒发现无解, 则可以直接返回.

   一种直观理解: 你和长度相同的其他木棒没区别.
   类似于3-2的证明, 只不过此时是几个断木棍长度之和与当前断木棍相同.
   反证法: 假设此时不考虑最后一个断木棍, 考虑其他后续木棍, 最终找到一个合法方案.
   说明当前断木棍和当前的木棒都拼接完毕. 由于当前断木棍可以和木棒拼接, 则交换位置后
   仍是合法方案, 矛盾. (描述有点模糊, 可以见下图)

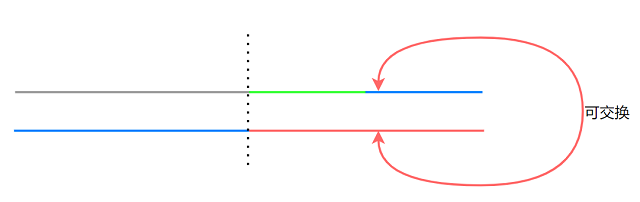
(灰色部分表示断木棍之前的方案已经固定 — 对应节点在当前节点上方)

具体代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 70;

int n, sum, length;
int w[N];
bool st[N];

bool dfs(int u, int s, int start)
{
    if (u * length == sum)  return true;
    if (s == length)    return dfs(u + 1, 0, 0);

    //i从start开始: 3.1-删除等效冗余
    for ( int i = start; i < n; i ++ )
    {
        if ( st[i] )   continue;
        if ( s + w[i] > length )    continue; //1.2-可行性搜索

        st[i] = true;
        if ( dfs(u, s + w[i], i + 1) )  return true;
        st[i] = false;

        //3.3-删除等效冗余
        if ( !s )   return false;

        //3.4-删除等效冗余
        if (s + w[i] == length) return false;

        //3.2
        int j = i + 1;
        while (j < n && w[j] == w[i])   j ++;
        i = j - 1;
    }
    return false;
}

int main()
{
    while (cin >> n, n)
    {
        sum = 0;
        memset(st, 0, sizeof st);

        for ( int i = 0; i < n; i ++ )
        {
            cin >> w[i];
            sum += w[i];
        }

        // 2-优化搜索顺序
        sort(w, w + n);
        reverse(w, w + n);

        for (length = w[0]; ; length ++)
        {
            if (sum % length == 0 && dfs(0, 0, 0))
            { //1.1-可行性搜索
                cout << length << endl;
                break;
            }
        }
    }
    return 0;
}