题目描述

天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。

如果一个星星的左下方（包含正左和正下）有 k 颗星星，就说这颗星星是 k 级的。

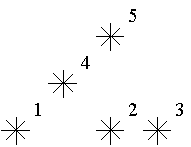
例如，上图中星星 5 是 3 级的（1,2,4 在它左下），星星 2,4 是 1 级的。

例图中有 1 个 0 级，2 个 1 级，1 个 2 级，1 个 3 级的星星。

给定星星的位置，输出各级星星的数目。

换句话说，给定 N 个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。

输入格式
第一行一个整数 N，表示星星的数目；

接下来 N 行给出每颗星星的坐标，坐标用两个整数 x,y 表示；

不会有星星重叠。星星按 y 坐标增序给出，y 坐标相同的按 x 坐标增序给出。

输出格式
N 行，每行一个整数，分别是 0 级，1 级，2 级，……，N−1 级的星星的数目。

数据范围
1 ≤ N ≤ 15000,
0 ≤ x,y ≤32000

样例

输入样例：

5
1 1
5 1
7 1
3 3
5 5

输出样例：

1
2
1
1
0

算法（复述y总的讲解）

从题目中可以得知 “不会有星星重叠，星星按 y 坐标增序给出，y 坐标相同的按 x 坐标增序给出。”
所以这题看似是二维的，其实可以当成一维的来做。输入过程中每输入一个坐标，那么前面输入的所有坐标中x坐标小于当前的x坐标的所有星星数就是当前这个星星的级数。这就等价于求[1,x)的区间和, 那么就可以用树状数组来做。

C++ 代码

#include <iostream>
#include <cstdio>
using namespace std;

const int  M = 32010;

int n;
int tr[M],num[M];

int lowbit(int x)
{
    return x & (-x);
}

void add(int x)
{
    for (int i = x; i <= M; i += lowbit(i)) tr[i] ++;
}

int query(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
    cin >> n;
    int t = n;
    while(t --)
    {
        int x, y;
        scanf("%d%d",&x,&y);
        x++;    //x可能是0，而树状数组起始是1
        num[query(x)] ++; //级数是query(x)的星星数量加一
        add(x);
    }

    for (int i = 0; i < n; i ++) printf("%d\n",num[i]);

    return 0;
}