前缀和博客链接

第八届2017年蓝桥杯真题

AcWing 1230. K倍区间

JavaB组第10题

一维前缀和

某一段连续的区间是k的倍数

我们看第一个样例：

输入样例：

5 2
1
2
3
4
5

输出样例：

6

求5个数某一段连续的区间是2的倍数有多少

长度是1：2，4 2个

长度是2： 0个

长度是3：[1, 3] [3, 5] 2个

长度是4：[1, 4] [2, 5] 2个

长度是5： 0个

总和是6，输出6。

暴力枚举（超时）

最朴素做法

时间复杂度$O(N^3)$

超时，AcWing只过了6/11个数据，蓝桥杯过了2/7个数据，满分100分我只拿到了28分

import java.util.Scanner;

public class Main {

    static final int N = 100010;
    static int[] a = new int[N];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int k = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            a[i] = sc.nextInt();
        }
        int res = 0;
        for (int r = 1; r <= n; r++) { // 右端点
            for (int l = 1; l <= r; l++) { // 左端点 
                int sum = 0;
                for (int i = l; i <= r; i++) {
                    sum += a[i];
                }
                if (sum % k == 0) res++;
            }
        }
        System.out.print(res);
    }
}

前缀和优化（超时）

时间复杂度$O(N^2)$

但并没有什么用，AcWing还是超时，蓝桥杯的测评结果跟暴力枚举拿的分一样，我以为能骗到更多的分，这就很懵了

import java.util.Scanner;

public class Main {

    static final int N = 100010;
    static int[] a = new int[N]; // 原数组
    static int[] s = new int[N]; // 前缀和数组

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int k = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            a[i] = sc.nextInt();
            s[i] = s[i - 1] + a[i]; // 公式一
        }
        int res = 0;
        for (int r = 1; r <= n; r++) { // 右端点
            for (int l = 1; l <= r; l++) { // 左端点 
                int sum = s[r] - s[l - 1]; // 公式二
                if (sum % k == 0) res++;
            }
        }
        System.out.print(res);
    }
}

AcWing评测结果

蓝桥杯评测结果

用前缀和干掉了一层循环，但并没有达到我们想要的结果，那我们从哪方面还可以优化呢？

前缀和 + 数学 优化（AC）

时间复杂度$O(N)$

我们可以再干掉一层循环。

当R固定时，在1 ~ R之间找到有多少个L满足(s[R] - s[L - 1]) % k == 0

这其实就是我们第二层循环的含义，我们将循环条件简单的变一下：

当R固定时，在0 ~ R - 1之间找到有多少个L满足(s[R] - s[L]) % k == 0
可转换为：s[R] % k == s[L] % k

即有多少个S[L]与S[R]的余数相同

我们可以开一个新的数组，cnt[i]，表示余数是i的数有多少个

for(int R = 1; R <= n; R++) {
    res += cnt[s[R] % k];
    cnt[s[R] % k]++;
}

完整代码 AcWing AC 蓝桥杯满分

时间复杂度$O(N)$

import java.util.Scanner;

public class Main {

    static final int N = 100010;
    static long[] s = new long[N]; // 前缀和数组 要开成long 防止爆int
    static int[] cnt = new int[N]; // 存每个余数的个数数组 

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int k = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            s[i] = s[i - 1] + sc.nextInt(); // 公式一 直接一步到位 不需要原数组存值
        }
        long res = 0;
        cnt[0] = 1; // cnt[0]中存的是s[]中等于0的数的个数 由于s[0] = 0 所以最初等于0的有1个数 所以cnt[0] = 1 详见下图
        for (int r = 1; r <= n; r++) { // 数学思想优化公式二
            /* 
                推荐输出以下语句：能看到以r结尾的k倍区间个数
                1 0 --> 1%2=1  前面有0个1 res+0
                2 1 --> 3%2=1  前面有1个1 res+1
                3 1 --> 6%2=0  前面有1个0 res+1 
                4 2 --> 10%2=0 前面有2个0 res+2
                5 2 --> 15%2=1 前面有2个1 res+2
            */
            //System.out.println(r + " " + cnt[(int)(s[r] % k)]);
            res += cnt[(int)(s[r] % k)];
            cnt[(int)(s[r] % k)]++; // 记录序列%k不同余数的个数
        }
        System.out.print(res);
    }
}

cnt[0]为什么要赋值为1？

因为我们的思路是找到两个序列和s[R] % k和s[L] % k的余数相同的个数，而我们的前缀和一般式不包含s[0]这个东西的，因为它的值是0，在前缀和中没有意义，但是这道题有意义，样例里面前缀和序列%k之后是1 1 0 0 1，两两比较，我们只能找到四个，如下图：

不加cnt[0] = 1，res的值为4

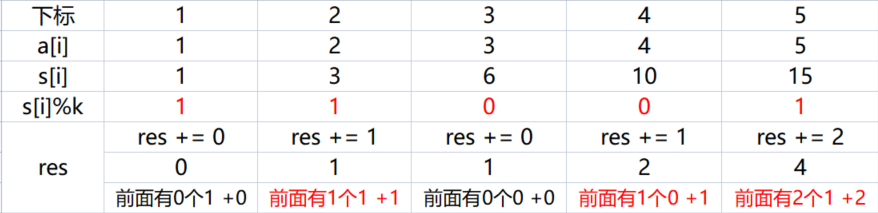
为什么少了两个？因为我们不一定需要两个序列，单个序列取余==0也构成k倍区间，此时我们就要假设s[0] = 0是有意义的；

我们cnt[0]中存的是s[]中等于0的数的个数，由于s[0] = 0，所以最初等于0的有1个数，所以cnt[0] = 1。

加上cnt[0] = 1，res的值为6

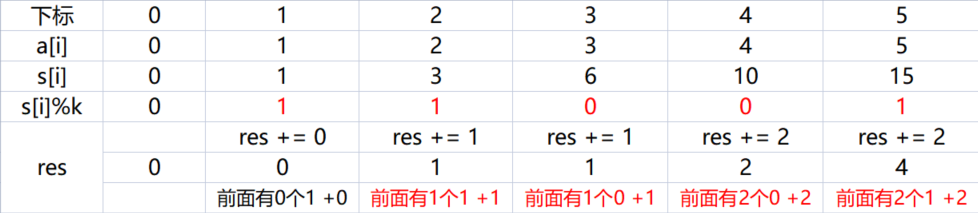
蓝桥杯满分

本题优化：$O(N^3) → O(N^2) → O(N) $

参考白線流つ