算法

(数位统计) $O(mlogn)$

相似题目：剑指offer | 整数中1出现的次数（从1到n整数中1出现的次数）（数位统计 logN复杂度 C++）
（1）求 $a$ 到 $b$ 之间的 $k$ 的个数（k = [0,..9]），我们只要统计从 $1$ 到 $a - 1$ 的 $k$ 的个数，从 $1$ 到 $b$ 的 $k$ 的个数，然后让他们相减即可
（2） 而统计从 $1$ 到 $n$ 的 $k$ 的个数的方法可以看【剑指offer | 整数中1出现的次数】传送门 这个题。

需要注意的是，当$k = 0$ 时我们要删去一部分数，例如，abcdef，统计c这个位置上为k的个数，如果$k=0$，则我们算$00\sim ab-1$的情况时(res += left * t;)，会把000def这种情况算进去，但实际上这时的数字只有def，所以需要减去这部分数，即if (k == 0) res -= t

（3）注意 $a$ 大于 $b$ 时要交换它们

图解：以统计从 $1$ 到 $n$ 的 $1$ 的个数为例

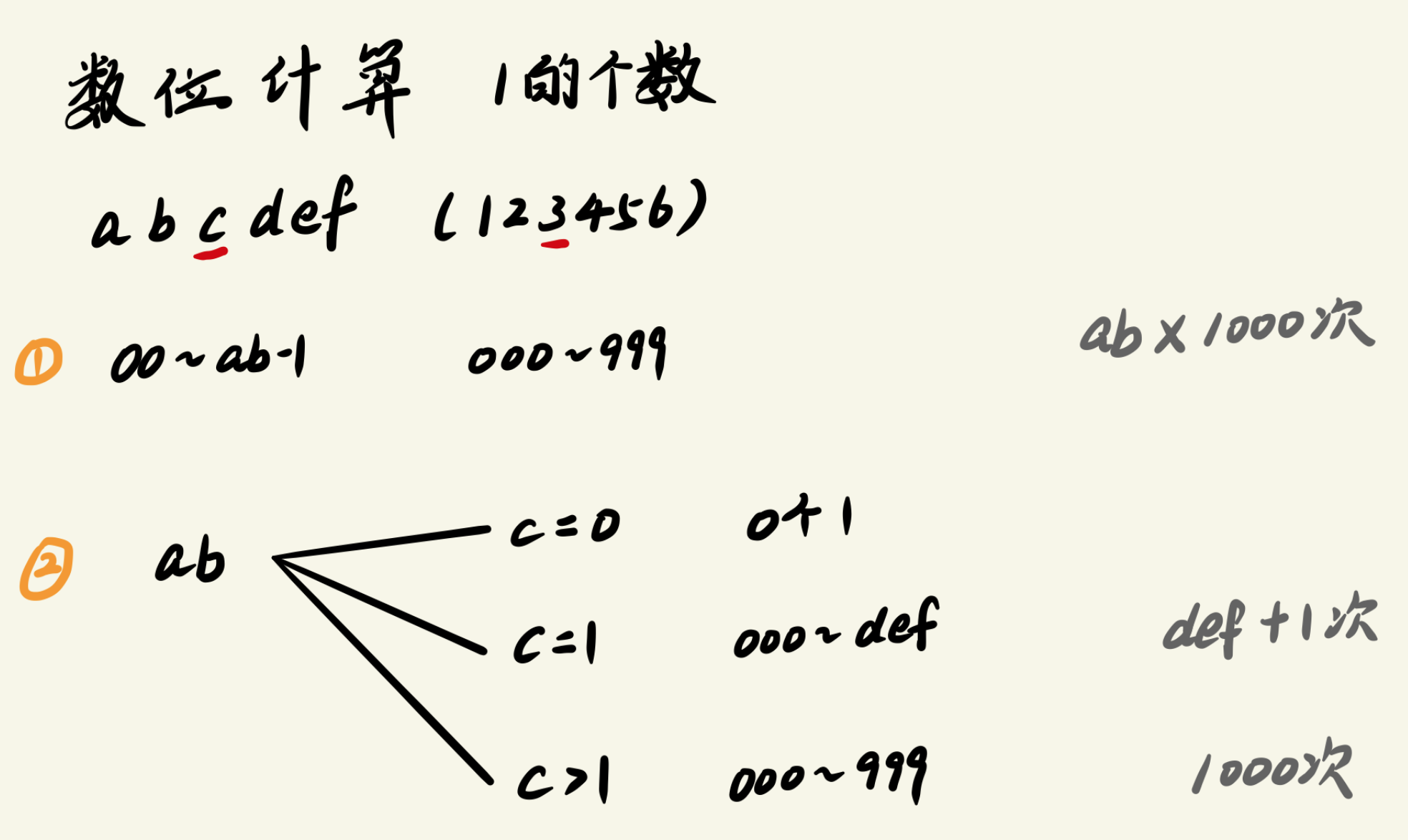
时间复杂度是$O(mlogn)$：m为询问的次数，空间复杂度是$O(logn)$

C++代码

#include <iostream>
#include <vector>

using namespace std;

// Get the number of k from 1 to n
int kNumbers(int n, int k) {
    if (!n) return 0;
    // n = 123 answer = [3, 2, 1]
    vector<int> answer; 
    while(n) answer.push_back(n % 10), n /= 10;

    int res = 0;
    for (int i = answer.size() - 1; i >= 0; i --) {
        int left = 0, right = 0, t = 1;
        for (int j = answer.size() - 1; j > i; j --) left = left * 10 + answer[j];
        for (int j = i - 1; j >= 0; j --) right = right * 10 + answer[j], t *= 10;

        res += left * t;
        if (k == 0) res -= t; // 0 is special
        if (answer[i] == k) res += right + 1;
        if (answer[i] > k) res += t;
    }
    return res;
}

int main() {
    int a, b;
    int A[10], B[10]; // A[i] means the number of i from 1 to a 

    while(cin >> a >> b && a != 0 && b != 0) {
        if (a > b) swap(a, b);

        for (int i = 0; i < 10; i ++) {
            A[i] = kNumbers(a - 1, i);
            B[i] = kNumbers(b, i);
            cout << B[i] - A[i] << " ";
        }
        cout << endl;
    }


    return 0;
}