原题传送门

欢迎各位大佬来踩！

这题是lxl 由乃上课时讲的一道例题，刚听了回放，参考了一下题解写出了本文。

Part 0 对题目的理解

lxl yyds！

以上出自lxl的课件。

Part 1 想法

以上还是出自lxl的课件。

让我们来说人话。

1. 首先，对于每一个不等式$ax+b > c$，我们可以把它转换成一个分式$x > (c-b)/a$。由于a可能为负，我们需要分类讨论。
2. 又$∵x(也就是k)$ $∈$ $[$ −$10^6$ $,$ $10^6$ $]$，$∴$我们要开两个值域上的树状数组。
3. 当$x > (c-b)/a$时，x > floor((c*1.0-b)/a)，即下取整的$(c-b)/a$。同理当$x < (c-b)/a$时，x < ceil((c*1.0-b)/a)，即上取整的$(c-b)/a$。

那么所谓注意细节指的是什么呢。

Part 2 “注意细节”

1. a有可能为0，需要特判，否则会RE
2. 对于一些恒成立或恒不成立的不等式，需要特殊记录
3. 树状数组防负数需要离散化
4. 下取整和整除是两个概念。我之前就一直搞不懂还特意发了个铁汁。如果您还是不明白我放两张图直观感受一下。

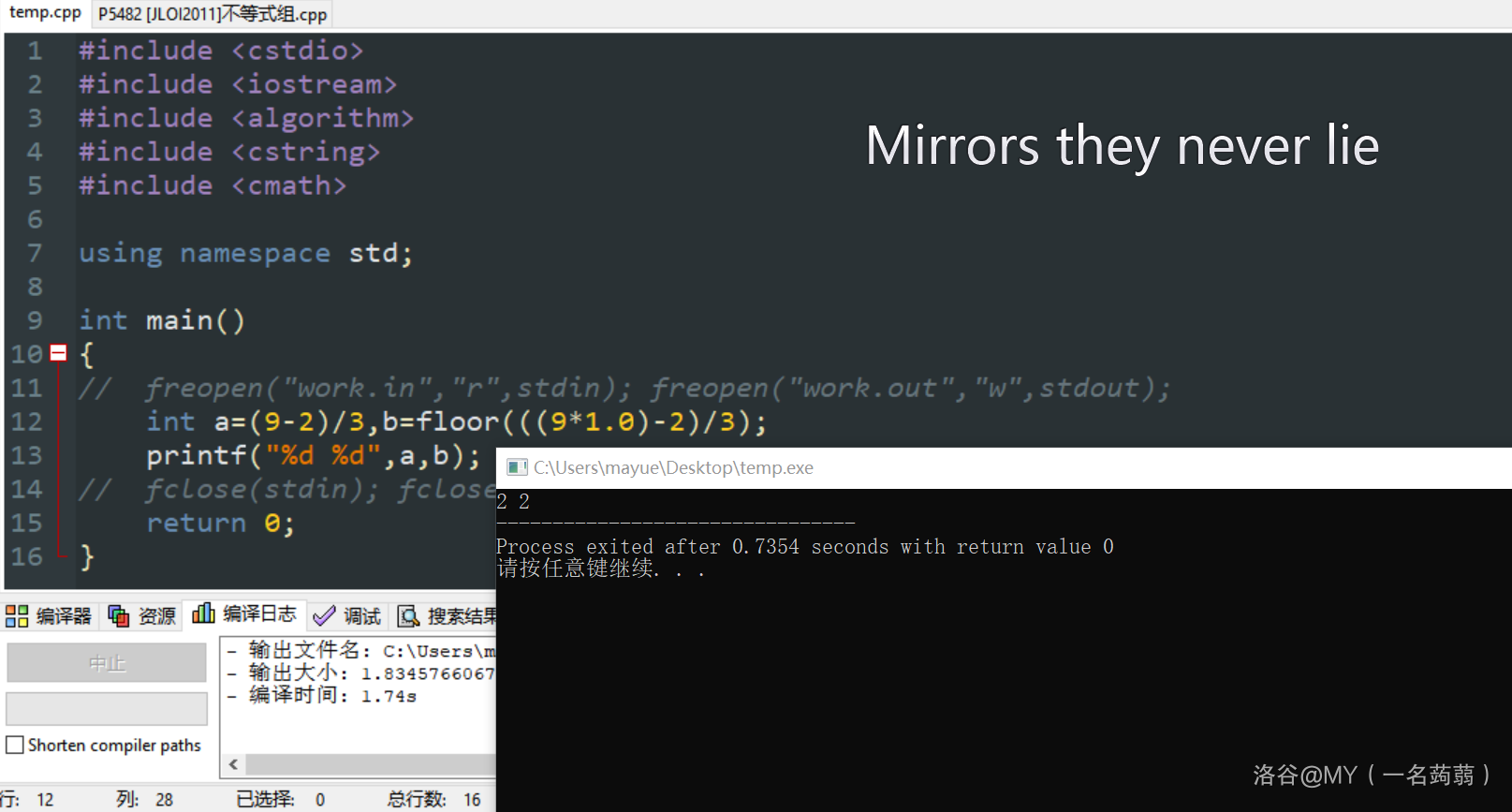
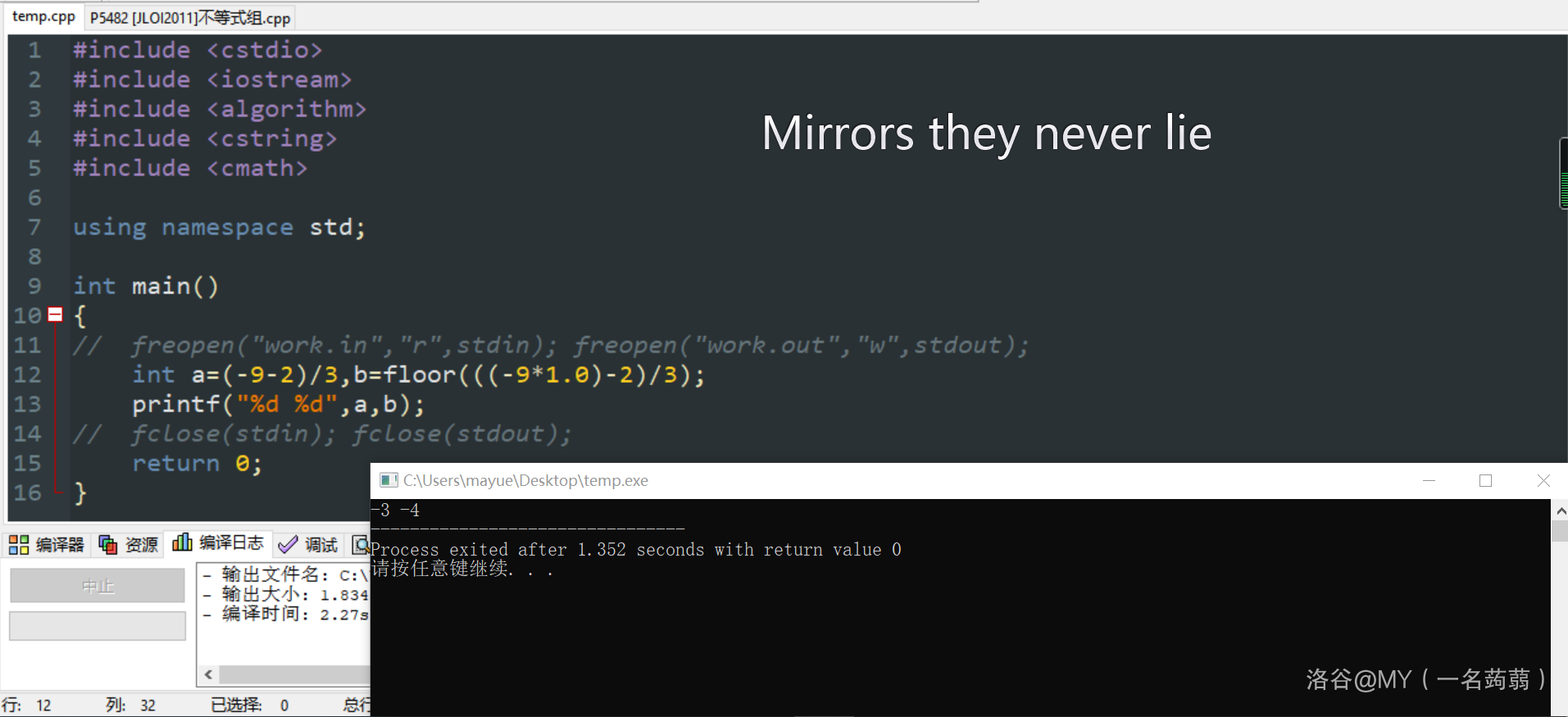
Part 3 Code

具体的注释在代码里了，请结合讲解食用。

//分类思想+转化思想 
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <cstdlib>

using namespace std;

const int N=1e6+10,M=1e5+10;

int n,C[N*2],c[N*2],top,kind[M],k[M],cnt;
//kind：哪一类不等式；  k：不等式合法需要的 k (k=(c-b)/a)；
//C/c：两类不等式（k < x | k > x） 
//cnt：恒成立不等式个数； 
bool used[M];//记录这个不等式是否被删除 
char s[20];

void modify(int x,int y,int t[])//不要问我为什么起这个名字，问就是lxl 
{
    x+=N;//防负数 
    for(;x<=2e6+10;x+=x&(-x))//lowbit(x)=x&(-x)
        t[x]+=y;
    return ;
}

int sum(int x,int t[])
{
    x+=N;
    int res=0;
    for(;x;x-=x&(-x))
        res+=t[x];
    return res;
}

int main()
{
//  freopen("work.in","r",stdin); freopen("work.out","w",stdout);
    scanf("%d",&n);
    int x,y,z;
    while(n--)
    {
        while(1)
        {
            scanf("%s",s);//输入操作 
            if(s[0] == 'A' || s[0] == 'Q' || s[0] == 'D')
                break ;
        }
        if(s[0] == 'A')
        {
            scanf("%d%d%d",&x,&y,&z);
            if(!x)//x=0 不等式转化为 b > c 
            {
                if(y > z)
                {
                    cnt++;
                    kind[++top]=3;//表示恒成立 
                }
                else kind[++top]=0;//恒不成立
            }
            if(x > 0)//x > (c-b)/a
            {
                k[++top]=floor((z*1.0-y)/x);//下取整 
                kind[top]=1;//表示合法的 k < x
                //k < x 且k已经上溢  
                if(k[top] > 1e6) kind[top]=0;//表示恒不成立 
                else if(k[top] < -1e6)//k < x 且k已经下溢 
                {
                    cnt++;//恒成立 
                    kind[top]=3;
                }
                else modify(k[top],1,C);
            }
            if(x < 0)//同理，可类比上面理解
            {
                k[++top]=ceil((z*1.0-y)/x);
                kind[top]=2;
                if(k[top] < -1e6) kind[top]=0;
                else if(k[top] > 1e6)
                {
                    cnt++;
                    kind[top]=3;
                }
                else modify(k[top],1,c);
            }
        }
        if(s[0] == 'Q')
        {
            scanf("%d",&x);
            printf("%d\n",sum(x-1,C)+(sum(1e6,c)-sum(x,c))+cnt);
            //合法的(k < x) + 合法的(k > x) + 恒成立 
        }
        if(s[0] == 'D')//Delete
        {
            scanf("%d",&x);
            if(used[x]) continue ;
            used[x]=true;
            if(kind[x] == 3) cnt--;
            if(kind[x] == 1) modify(k[x],-1,C);
            if(kind[x] == 2) modify(k[x],-1,c);
        }
    }
//  fclose(stdin); fclose(stdout);
    return 0;
}

Thank you for your reading!