题目描述

二叉树上有 n 个结点，按从 0 到 n - 1 编号，其中结点 i 的两个子结点分别是 leftChild[i] 和 rightChild[i]。

只有 所有 结点能够形成且 只 形成 一颗 有效的二叉树时，返回 true；否则返回 false。

如果结点 i 没有左子结点，那么 leftChild[i] 就等于 -1。右子结点也符合该规则。

注意，结点没有值，本问题中仅仅使用结点编号。

样例

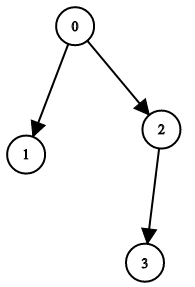
输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
输出：true

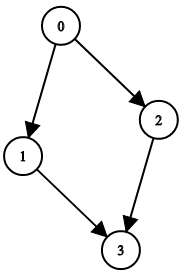
输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
输出：false

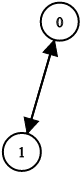
输入：n = 2, leftChild = [1,0], rightChild = [-1,-1]
输出：false

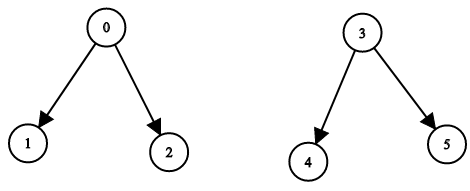
输入：n = 6, leftChild = [1,-1,-1,4,-1,-1], rightChild = [2,-1,-1,5,-1,-1]
输出：false

限制

• 1 <= n <= 10^4
• leftChild.length == rightChild.length == n
• -1 <= leftChild[i], rightChild[i] <= n - 1

算法

(树的性质，深度优先遍历) $O(n)$

满足一下条件才能证明是一棵有根树。

1. 有向边的数量等于结点的数量减 1。
2. 每个结点的入度小于等于 1。
3. 1 和 2 共同证明了仅存在一个入度为 0 的结点，因为所有结点的入度和等于有向边的个数。此时，还需要判断，从这个入度为 0 的结点，是否可以访问到所有的结点。这是为了排除一棵树和若干个环的情况。

时间复杂度

• 共有 $O(n)$ 条有向边，且最后遍历时每个结点最多访问一次，故总时间复杂度为 $O(n)$。

空间复杂度

• 需要额外 $O(n)$ 的空间存储每个点的入度和深度优先遍历的系统栈。

C++ 代码

class Solution {
public:
    int dfs(int x, const vector<int>& leftChild, const vector<int>& rightChild) {
        if (x == -1) return 0;

        return dfs(leftChild[x], leftChild, rightChild)
             + dfs(rightChild[x], leftChild, rightChild)
             + 1;
    }

    bool validateBinaryTreeNodes(int n,
        vector<int>& leftChild, vector<int>& rightChild) {

        vector<int> indegree(n, 0);
        int m = 0;

        for (int i = 0; i < n; i++) {
            if (leftChild[i] > -1) {
                m++;
                indegree[leftChild[i]]++;
            }

            if (rightChild[i] > -1) {
                m++;
                indegree[rightChild[i]]++;
            }
        }

        if (m != n - 1)
            return false;

        int rt = -1;
        for (int i = 0; i < n; i++) {
            if (indegree[i] == 0)
                rt = i;
            else if (indegree[i] > 1)
                return false;
        }

        return dfs(rt, leftChild, rightChild) == n;
    }
};