AcWing 788. 逆序对的数量

给定一个长度为n的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i < j 且 a[i] > a[j]，则其为一个逆序对；否则不是。

输入格式
第一行包含整数n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式
输出一个整数，表示逆序对的个数。

数据范围
1≤n≤100000
输入样例：
6
2 3 4 5 6 1
输出样例：
5

#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int keep[N];
long long int res = 0;


void merge_sort(int q[],int l,int r)//归并排序
{
    if(l==r) return;
    int mid = l+r >> 1;
    merge_sort(q,l,mid),merge_sort(q,mid+1,r);
    int i = l,j = mid+1,k = 0;

    while(i<=mid&&j<=r)
    {
        if(q[i]<=q[j]){
            keep[k++] = q[i++];

        }else{
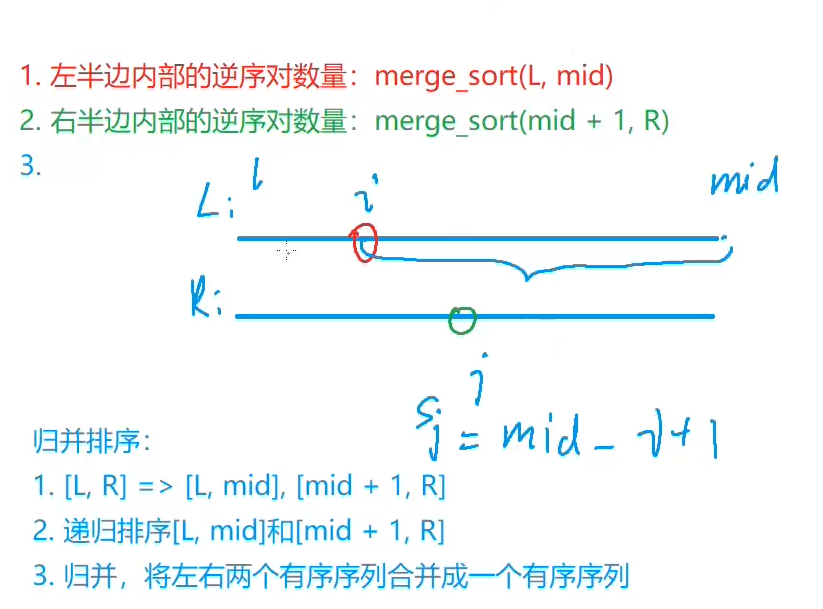
             res += mid-i+1;//敲重点！！求得两端，其中后一段a[j]小于前一段a[i]后面一部分Sj,依此类推
            keep[k++]= q[j++];
        }
    }
    //结尾，结束后面多出来的一段尾巴，看那一段作为主段
    while(i<=mid) keep[k++] = q[i++];
    while(j<=r) keep[k++] = q[j++];
    //物归原主
    for(int i = l,j = 0;i<=r;i++,j++)q[i] = keep[j];

}

int main(){
    int n;
    cin>>n;
    int q[N];
    for(int i = 0;i<n;i++)scanf("%d",&q[i]);
    merge_sort(q,0,n-1);//利用归并排序求得逆序对的数量
    cout<<res<<endl;
    return 0;
}