算法分析

与AcWing 1222. 密码脱落 分析方式类似

从当前BE变成GBE需要添加最少字符的数量 等价于 当前Be变成最大的GBE需要去掉字符的数量
即至少添加最少字符 等价于 总数量 - 最大GBE子序列的长度

注意：这题和密码脱落也有些不同，GBE有回文的性质 或者 有另外一种性质，例如[]() , ([])均是GBE，因此需要对s[L] 和 s[R]不匹配的情况需要进一步划分，划分方式和石子合并类似

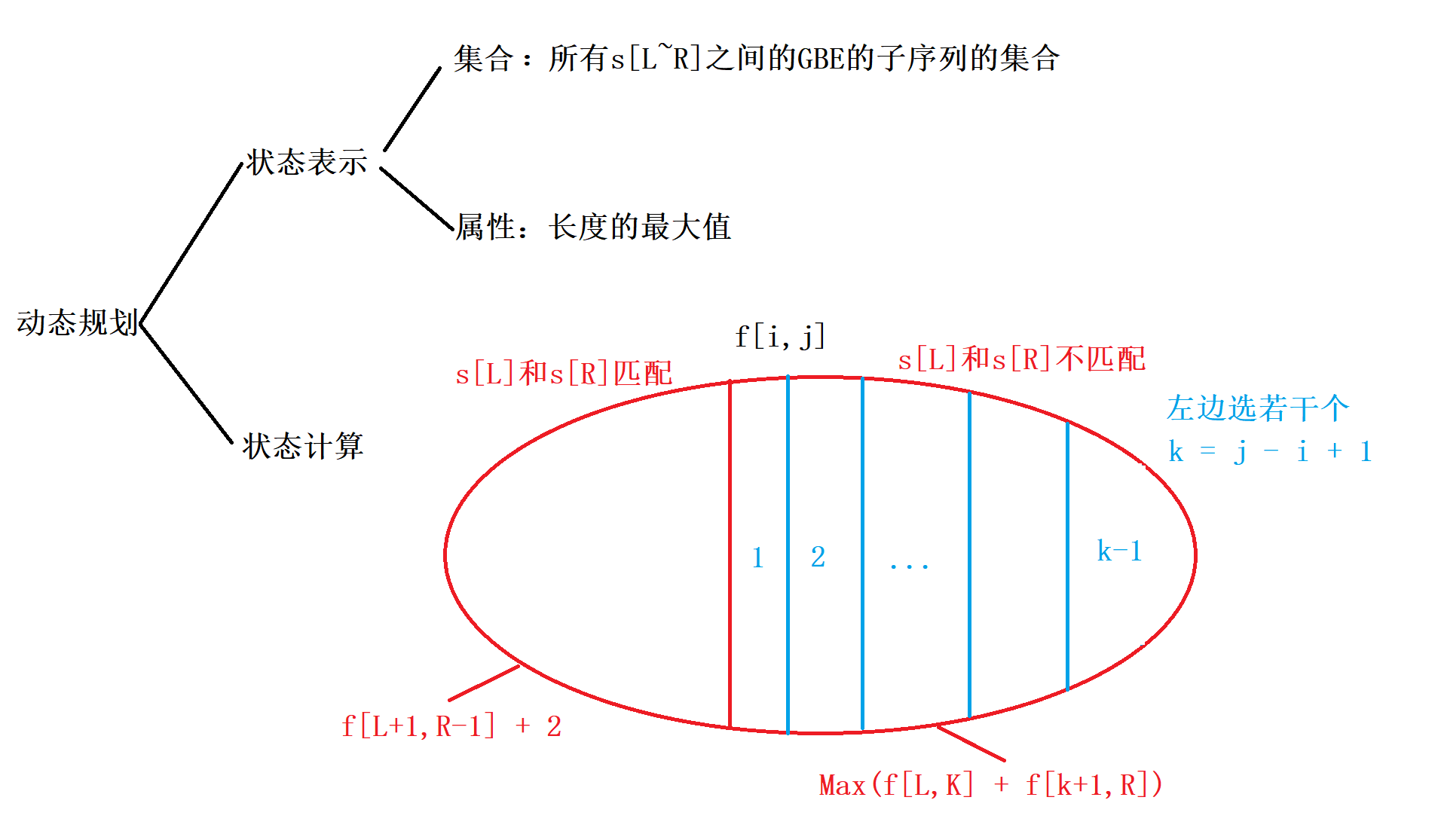
时间复杂度 $O(n^3)$

Java 代码

import java.util.Scanner;

public class Main {
    static int N = 110;
    static int n;
    static String s;
    static int[][] f = new int[N][N];
    static boolean check(char a,char b)
    {
        if(a == '(' && b == ')') return true;
        if(a == '[' && b == ']') return true;
        return false;
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        s = scan.next();
        n = s.length();
        for(int len = 2;len <= n;len ++)
        {
            for(int L = 0;L + len - 1 < n;L ++)
            {
                int R = L + len - 1;
                if(check(s.charAt(L),s.charAt(R))) f[L][R] = Math.max(f[L][R], 2 + f[L + 1][R - 1]); 
                for(int k = L;k <= R;k ++)
                {
                    f[L][R] = Math.max(f[L][R], f[L][k] + f[k + 1][R]);
                }
            }
        }
        System.out.println(n - f[0][n - 1]);
    }
}