分析

时间复杂度

状态数量 * 状态转移

$O(N^2 * N) ==> O(N^3)$

c++代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 110, inf = 0x3f3f3f3f;

char s[N];
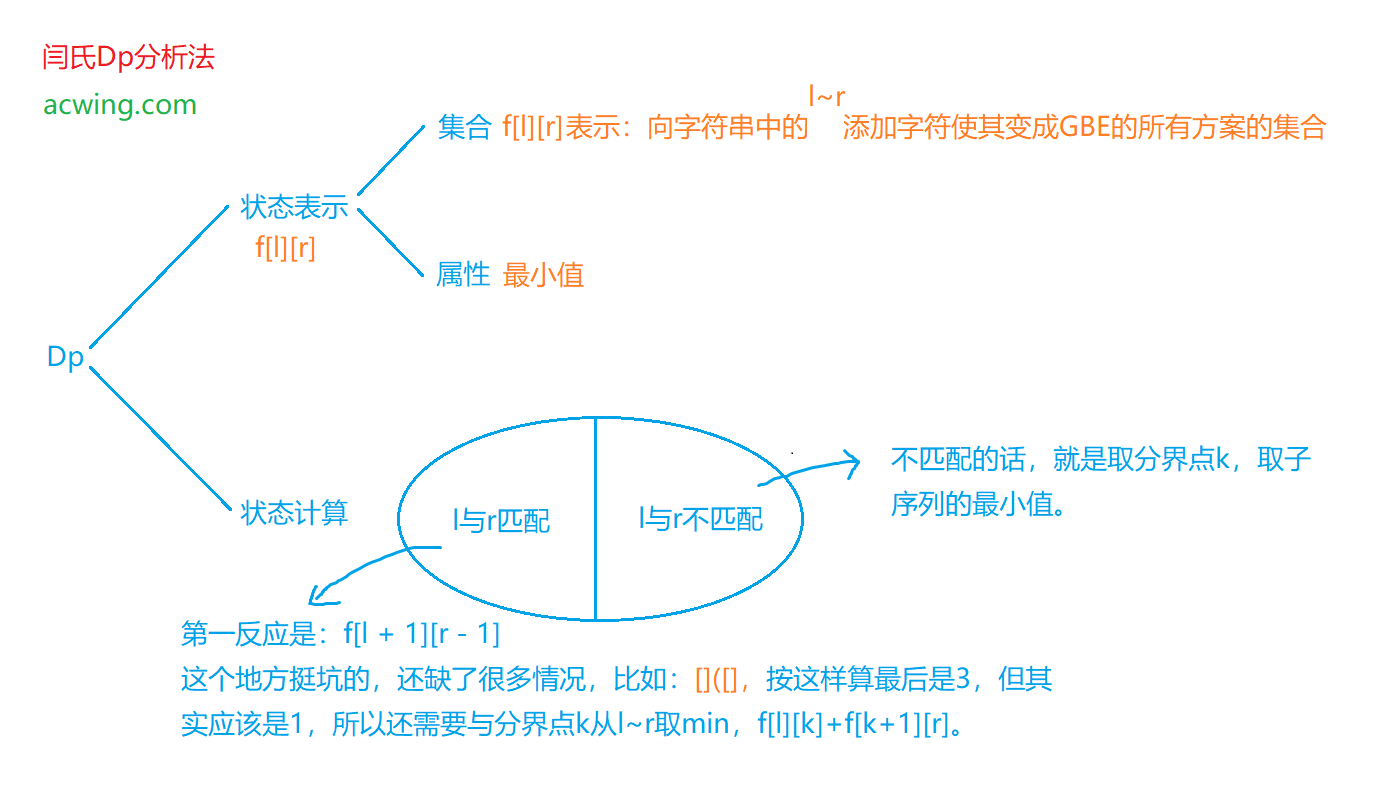
int f[N][N]; // f[i][j]代表将i~j个字符变成GBE的所有方案的集合的最小值

bool check(int a, int b)
{
    if (s[a] == '[' && s[b] == ']' || s[a] == '(' && s[b] ==')') return true;
    return false;
}

int main()
{
    scanf("%s", s + 1);
    int n = strlen(s + 1);

    for (int len = 1; len <= n; len++)
        for (int l = 1; l + len - 1 <= n; l++)
        {
            int r = l + len - 1;
            if (len == 1) f[l][r] = 1;
            else
            {
                f[l][r] = inf;
                if (check(l, r)) f[l][r] = min(f[l][r], f[l + 1][r - 1]);
                for (int k = l; k <= r; k++)
                    f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r]);
            }
        }

    cout << f[1][n] << endl;

    return 0;
}