算法分析

为了供应电力，要么在当前位置 i 建发电站，要么与另外的已经有电力供应的矿井 j 之间建立电网

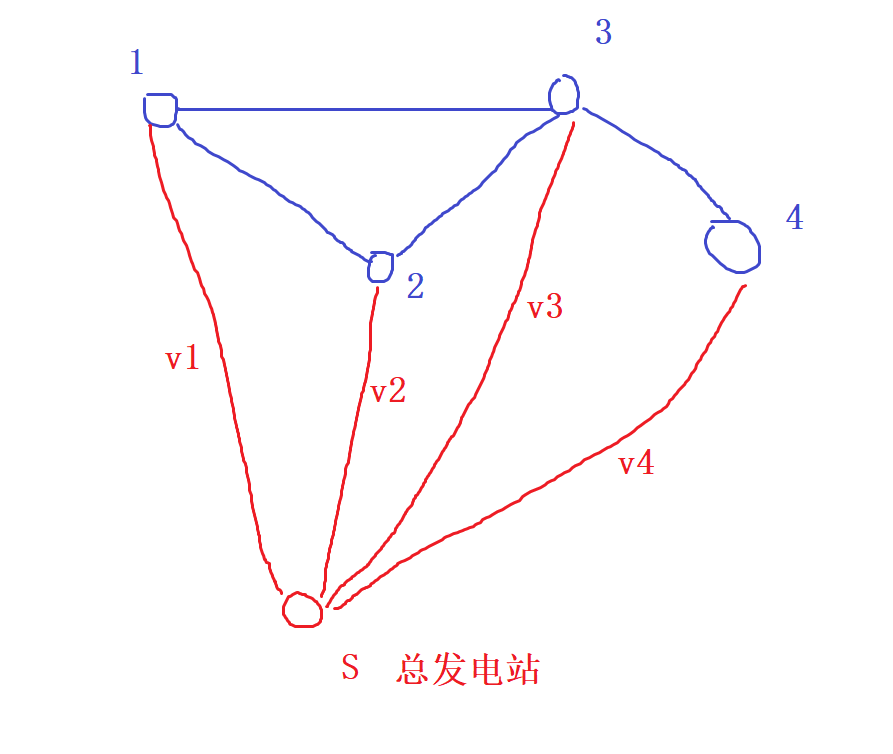
• 1、在当前位置i建发电站的费用是vi,建立虚拟结点S，相当于i号点到S号点的费用是vi

• 2、如图所示，求n个矿井电力供应的最小花费，等价于求n + 1个点的最小生成树

时间复杂度 $O(n^2)$

参考文献

算法提高课

Java 代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int N = 310;
    static int INF = 0x3f3f3f3f;
    static int n;
    static int[][] g = new int[N][N];
    static int[] dist = new int[N];
    static boolean[] st = new boolean[N];
    static int prim()
    {
        Arrays.fill(dist, INF);
        int res = 0;

        for(int i = 0;i < n + 1;i ++)
        {
            int t = -1;
            for(int j = 0;j <= n;j ++)
            {
                if(!st[j] && (t == -1 || dist[t] > dist[j]))
                    t = j;
            }

            if(i != 0 && dist[t] == INF) return INF;

            st[t] = true;

            if(i != 0) res += dist[t];

            for(int j = 0;j <= n;j ++) dist[j] = Math.min(dist[j],g[t][j]);
        }
        return res;
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        for(int i = 1;i <= n;i ++)
        {
            int w = scan.nextInt();
            g[0][i] = g[i][0] = w;
        }
        for(int i = 1;i <= n;i ++)
            for(int j = 1;j <= n;j ++)
            {
                g[i][j] = scan.nextInt();
            }

        System.out.println(prim());
    }
}