算法分析

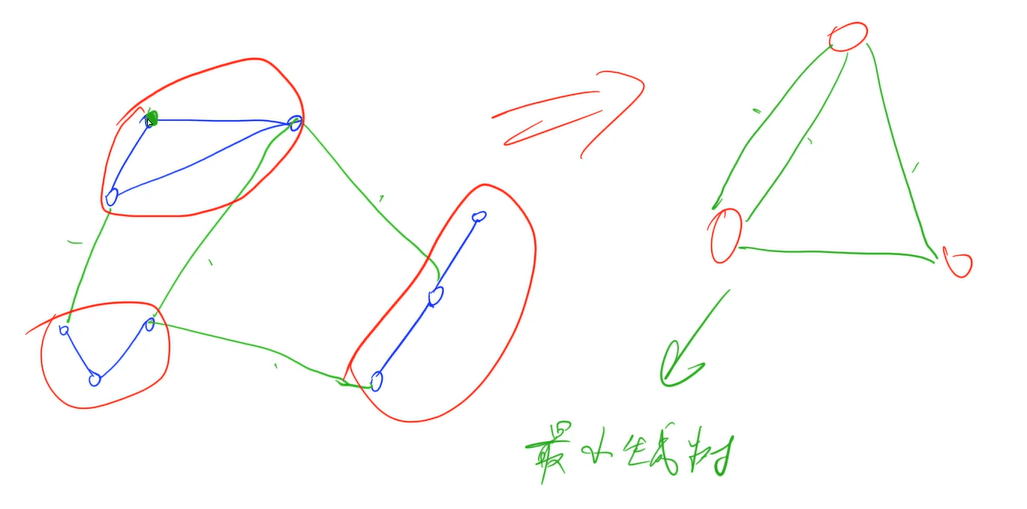
有两种通道，必选与非必选，花费最小费用使得所有点连通，即在必选边已经连接好的情况下，多个连通块通过非必选边合并成一棵最小生成树

如图所示，蓝色边是必选边，绿色边是非必选边，使用蓝色边形成一个连通块看出一个点，多个点求最小生成树

做法：kruskal

• 1、将所有必选边加到并查集中

• 2、将所有非必选边从小到大排序

• 3、从小到大依次枚举每一条非必选边，a,b,权值为w

  • 如果a和b不连通，将当前边选上，更新res

时间复杂度 $O(mlogm)$

参考文献

算法提高课

Java 代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int N = 2010,M = 10010;
    static int n,m;
    static int[] p = new int[N];
    static Edge[] edge = new Edge[M];
    static int find(int x)
    {
        if(p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        m = scan.nextInt();

        for(int i = 1;i <= n;i ++) p[i] = i;

        int res = 0,k = 0;
        for(int i = 0;i < m;i ++)
        {
            int t = scan.nextInt();
            int a = scan.nextInt();
            int b = scan.nextInt();
            int w = scan.nextInt();
            //必选边，缩点操作
            if(t == 1)
            {
                a = find(a);
                b = find(b);
                p[a] = b;
                res += w;
            }
            else
            {
                edge[k ++] = new Edge(a,b,w);
            }
        }

        Arrays.sort(edge,0,k);

        for(int i = 0;i < k;i ++)
        {
            int a = edge[i].a;
            int b = edge[i].b;
            int w = edge[i].w;
            a = find(a);
            b = find(b);
            if(a != b)
            {
                p[a] = b;
                res += w;
            }
        }
        System.out.println(res);

    }
}
class Edge implements Comparable<Edge>
{
    int a,b,w;
    Edge(int a,int b,int w)
    {
        this.a = a;
        this.b = b;
        this.w = w;
    }
    @Override
    public int compareTo(Edge o) {
        // TODO 自动生成的方法存根
        return Integer.compare(w, o.w);
    }
}