算法分析

区间dp

从当前样子变成初始状态需要添加叶子的数量 等价于 当前样子变成最大的回文串需要剪去的叶子的数量
即至少脱落多少个种子 等价于 总数量 - 最大回文子序列的长度

状态计算的选择方式和最长公共子序列类似

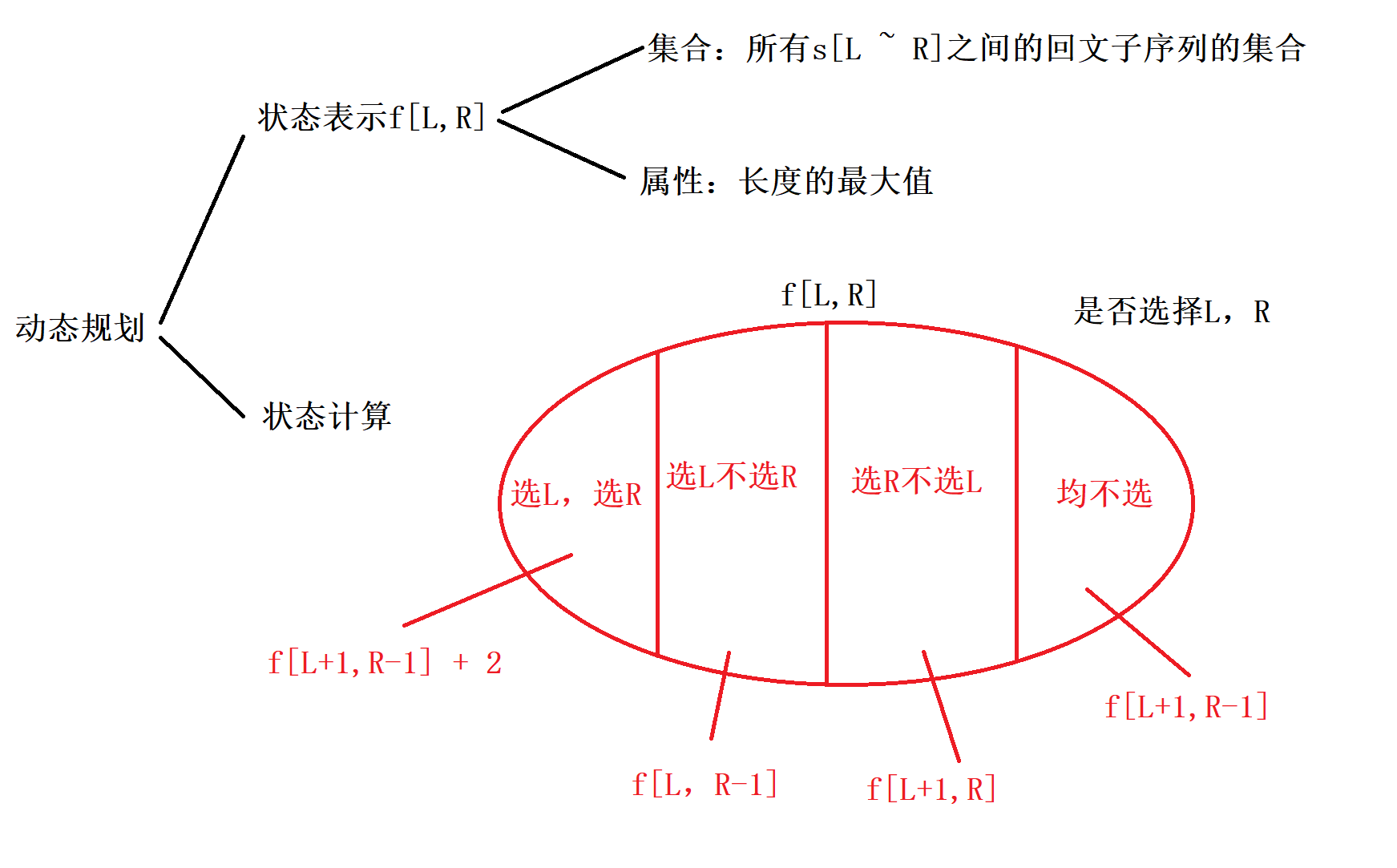
时间复杂度 $O(n^2)$

参考文献

蓝桥杯辅导课

Java 代码

import java.util.Scanner;

public class Main {
    static int N = 1010;
    static int[][] f = new int[N][N];
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        String s = scan.next();
        int n = s.length();
        for(int len = 1;len <= n;len ++)
        {
            for(int i = 0;i + len - 1 < n;i ++)
            {
                int j = i + len - 1;

                if(len == 1) f[i][j] = 1;
                else
                {
                    f[i][j] = Math.max(f[i][j - 1], f[i + 1][j]);
                    if(s.charAt(i) == s.charAt(j)) f[i][j] = Math.max(f[i][j], f[i + 1][j - 1] + 2);
                }
            }
        }
        System.out.println(n - f[0][n - 1]);
    }
}