算法1

dp

与AcWing 900. 整数划分类似

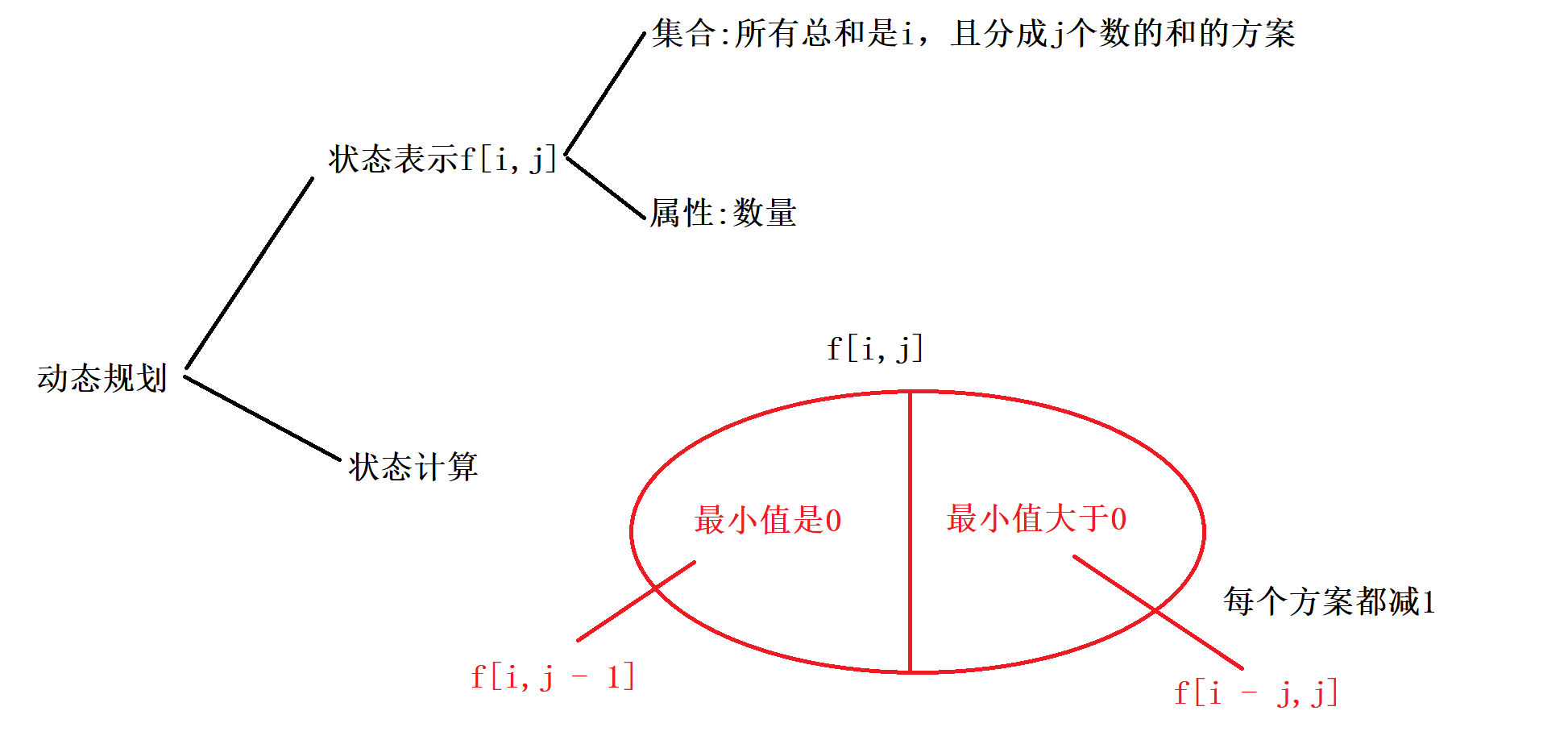
时间复杂度 $O(mn)$

参考文献

蓝桥杯辅导课

Java 代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int N = 1010;
    static int[][] f = new int[N][N];
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int T = scan.nextInt();
        while(T -- > 0)
        {
            int m = scan.nextInt();
            int n = scan.nextInt();
            for(int i = 0;i <= m;i ++) Arrays.fill(f[i], 0);
            f[0][0] = 1;
            for(int i = 0;i <= m;i ++)
                for(int j = 1;j <= n;j ++)
                {
                    f[i][j] = f[i][j - 1];
                    if(i >= j) f[i][j] += f[i - j][j];
                }
            System.out.println(f[m][n]);
        }
    }
}

算法2

爆搜
相当于是m个球，放n个盒子，每个盒子最少放0个球的问题

暴力枚举每个盒子放多少个球，为了方便从左到右的球的数量从小到大递增，dfs过程中需要添加多start作为开始枚举的位置

时间复杂度

具有各种剪枝和优化，很难分析

参考文献

蓝桥杯辅导课

Java 代码

import java.util.Scanner;

public class Main {
    static int n;
    static int m;
    static int ans = 0;
    //枚举第u个盒子，nums表示当前剩下多少个能量，从start数开始枚举
    static void dfs(int u,int nums,int start)
    {
        if(u == n + 1)
        {
            if(nums == 0) 
            {
                ans ++;
            }
            return;
        }
        if(start > nums) return;//可行性剪枝
        for(int i = start ;i <= nums;i ++)
        {
            dfs(u + 1,nums - i,i);
        }
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int T = scan.nextInt();
        while(T -- > 0)
        {
             ans = 0;
             m = scan.nextInt();//能量
             n = scan.nextInt();//分身个数
             dfs(1,m,0);
             System.out.println(ans);
        }
    }
}