题目描述

给你一个数组 events，其中 events[i] = [startDay_i, endDay_i]，表示会议 i 开始于 startDay_i，结束于 endDay_i。

你可以在满足 startDay_i <= d <= endDay_i 中的任意一天 d 参加会议 i。注意，一天只能参加一个会议。

请你返回你可以参加的 最大 会议数目。

样例

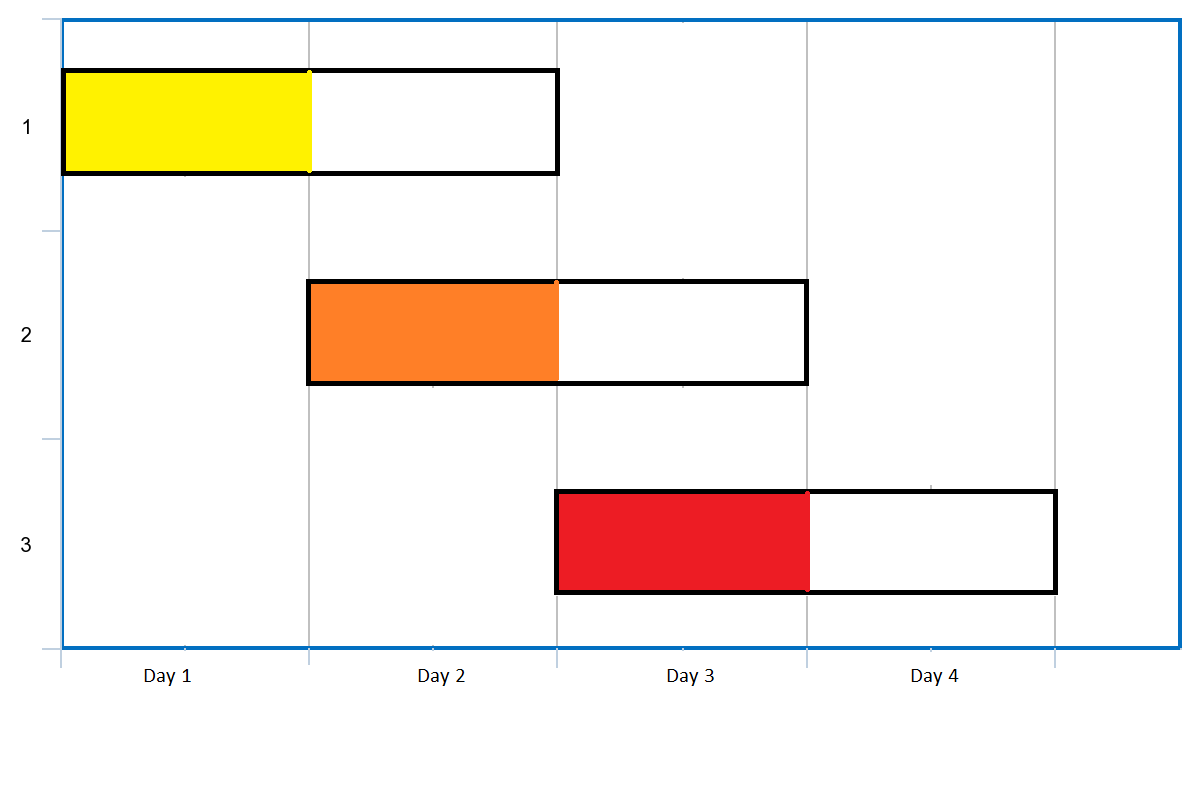
输入：events = [[1,2],[2,3],[3,4]]
输出：3
解释：你可以参加所有的三个会议。
安排会议的一种方案如上图。
第 1 天参加第一个会议。
第 2 天参加第二个会议。
第 3 天参加第三个会议。

输入：events= [[1,2],[2,3],[3,4],[1,2]]
输出：4

输入：events = [[1,4],[4,4],[2,2],[3,4],[1,1]]
输出：4

输入：events = [[1,100000]]
输出：1

输入：events = [[1,1],[1,2],[1,3],[1,4],[1,5],[1,6],[1,7]]
输出：7

限制

• 1 <= events.length <= 10^5
• events[i].length == 2
• 1 <= events[i][0] <= events[i][1] <= 10^5

算法1

(贪心，并查集) $O(n \log n + M)$

1. 将事件数组按照右端点从小到大排序。
2. 按顺序遍历每一个区间。试图找到当前区间左端点之后第一个没有被选中的位置 p，如果 p 小于等于右端点，则选中 p，答案加一。贪心的正确性可以简单说明下，由于右端点是单调不减的，所以放最左点是最保守的做法。如果整个区间的位置都被之前选过了，则当前区间无论如何都不可能和之前选中的区间共存。
3. 找第一个没被选中的位置，如果暴力做时间复杂度为 $O(M)$，虽然网站上不会超时，但这里有个更快的做法是用并查集。
4. 开一个下标从 1 到 M + 1 位置的并查集，初始化每个位置的父亲指向自己。如果选中了位置 p，则令集合 p 的父亲指向 p+1。我们每次可以通过寻找左端点的祖先，来快速获取第一个没有被访问过的位置。

时间复杂度

• 排序的时间复杂度为 $O(n \log n)$，并查集初始化的时间复杂度为 $O(M)$，其中 $M$ 为最大的日期。
• 遍历时，并查集的操作时间复杂度近似为常数，故总时间复杂度为 $O(n \log n + M)$。

空间复杂度

• 需要额外 $O(n)$ 的空间存储并查集。

C++ 代码

class Solution {
public:
    vector<int> f;
    int find(int x) {
        return x == f[x] ? x : f[x] = find(f[x]);
    }

    int maxEvents(vector<vector<int>>& events) {
        int n = events.size();
        sort(events.begin(), events.end(),
             [](const vector<int> &x, const vector<int> &y) {
                 return x[1] < y[1];
             }
        );

        int m = events.back()[1];
        f.resize(m + 2);

        for (int i = 1; i <= m + 1; i++)
            f[i] = i;

        int ans = 0;
        for (int i = 0; i < n; i++) {
            int x = find(events[i][0]);
            if (x <= events[i][1]) {
                ans++;
                f[x] = find(x + 1);
            }
        }

        return ans;
    }
};

算法2 （鸣谢 Spider ）

(贪心，小根堆) $O(n \log n)$

1. 将事件数组按照左端点从小到大排序，同时维护一个小根堆，以右端点为关键字存放事件编号。维护一个时间戳 cur。
2. 初始时，堆为空，时间戳为 0。我们每次从事件数组取事件放入小根堆中，然后从堆中选择一个结束最早的事件，然后时间戳向后移动。具体流程如下：
   • 循环条件，事件未完全遍历完或者堆未空。
   • 如果当前堆为空，则更新时间戳到第一个事件的开始时间。
   • 将所有等于当前时间戳的事件都放入小根堆。
   • 从小根堆中取出结束时间最早的事件，这个事件的处理时间就是 cur，然后 cur 加 1。
   • 如果小根堆中结束最早的时间小于了 cur，则说明这个事件没机会处理了，移出小根堆。
3. 贪心的正确性可以简要说明，由于每个事件的代价相等，所以对于每个时间点，我们都尽量按照结束时间最早的事件。如果存在一个最优的分配方案，满足某个时间点，有结束时间晚的任务先被完成，则总可以调换这两个任务的完成顺序而不影响结果。

时间复杂度

• 排序的时间复杂度为 $O(n \log n)$。
• 每个事件入堆一次，出堆一次，总时间复杂度为 $O(n \log n)$。
• 大的循环共执行 $O(n)$ 次，所以 cur 的更新次数不超过 $O(n)$ 次。
• 故总时间复杂度为 $O(n \log n)$。

空间复杂度

• 需要额外 $O(n)$ 的空间存储小根堆。

C++ 代码

class Solution {
public:
    int maxEvents(vector<vector<int>>& events) {
        int n = events.size();
        sort(events.begin(), events.end());

        auto cmp = [&](int x, int y) {
            return events[x][1] > events[y][1];
        };

        priority_queue<int, vector<int>, decltype(cmp)> heap(cmp);

        int i = 0, cur = 0, ans = 0;
        while (i < n || !heap.empty()) {
            if (heap.empty())
                cur = events[i][0];

            while (i < n && events[i][0] == cur)
                heap.push(i++);

            ans++;
            heap.pop();
            cur++;

            while (!heap.empty() && events[heap.top()][1] < cur)
                heap.pop();
        }

        return ans;
    }
};