算法提高课汇总

双向广搜

$bfs$的优化

$bfs$算法时间复杂度$O(V + E)$, 线性关系:

• 对于最短路模型, 所有顶点个数即网格数目, 边数为$4\times V$或$8\times V$, 一般无需优化.

• 对于最小步数模型, 整个网格图作为一个状态即顶点, 状态间的转换作为边, 此时状态数目可能很大,
  需要某些优化技巧.

例如对本题来说, 假设对于每个字符(作为一个顶点)其能扩展$K$个字符, 最多扩展$10$层,
则状态个数约为$K^{10}$. 如果不加优化会TLE或MLE.

双向广搜优化

双向广搜优化思路是从起点和终点同时扩展, 当相遇时即得到完整搜索路径.

优化原理: $bfs$的每一层相比上一层数目指数增加. 以本题为例, 若单向搜索, 最终状态个数为$K^{10}$,
而如果双向搜索, 平均下来两个方向只需搜索原层数的一半, 状态个数减少至$2\times K^5$.

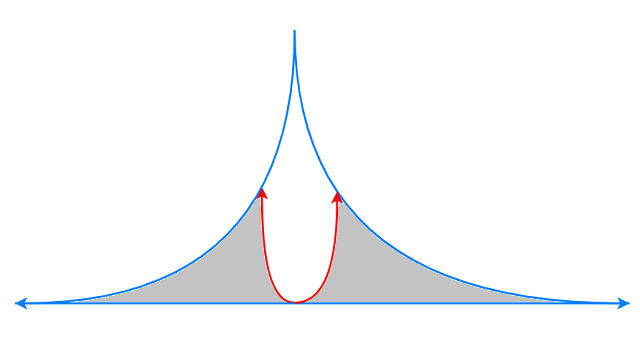
双向广搜队列扩展有两种方式:

1. 起点和终点依次各扩展一步.

2. 每步选择扩展队列中状态较小的方向.

采用第2种方式在平均意义上效果更好.

具体实现

本题可以看作 AcWing 1107. 魔板 的扩展: 状态数目更多, 需要优化.

• 在从终点扩展时, 状态转换规则需要反向应用. 此时扩展规则类似于有向边.

• 如果一方状态扩展完毕还未相遇, 表明从起点到终点并不连通.

  不存在一方扩展完毕未相遇(队列未空), 接着另一方向继续扩展, 最终相遇的情况.
  设最终相遇点为$v$, 如果此时最终仍能相遇, 则继续扩展的一方从点$u\rightarrow v$.
  此时$v\rightarrow u$不存在, 因为$v$在此之前已经扩展完毕.
  两者矛盾, 上述假设不成立.
  ($u\rightarrow v$, 一定也存在$v\rightarrow u$, 因为两者应用同一规则的两种顺序.)

具体代码

#include <queue>
#include <cstring>
#include <iostream>
#include <unordered_map>

using namespace std;

typedef unordered_map<string, int> umap;

const int N = 6, MAX_STEP = 10;

int n;
string a[N], b[N]; //变换规则

//扩展一步. q: 扩展队列; a -> b 扩展规则
//返回数值 <= 10: 成功相遇; > 10 : 未相遇
int extend(queue<string> &q, umap &da, umap &db, string a[], string b[])
{
    string s = q.front(); q.pop();
    for( int i = 0; i < n; i ++ )//变换规则
    {
        for( int j = 0; j < s.size(); j ++ ) //变换位置
        {
            if( s.substr(j, a[i].size()) == a[i] )
            {//可以应用规则
                string t = s.substr(0, j) + b[i] + s.substr(j + a[i].size());

                if( db.count(t) ) return da[s] + 1 + db[t]; //相遇

                if( !da.count(t) )
                {//还未扩展t
                    da[t] = da[s] + 1;
                    q.push(t);
                }
            }
        }
    }
    return MAX_STEP + 1; //还未相遇
}

int bfs(string A, string B)
{
    if( A == B )    return 0; //特殊情况 无需扩展

    queue<string> qa, qb; //两个方向扩展
    umap da, db;
    qa.push(A), da[A] = 0;
    qb.push(B), db[B] = 0;

    //如果一方已扩展完毕仍未相遇 表明不存在A->B的路径
    while( qa.size() && qb.size() ) 
    {
        int step;
        //扩展队列状态较小的方向
        if( qa.size() < qb.size() ) step = extend(qa, da, db, a, b);
        else    step = extend(qb, db, da, b, a); //距离数组: db, da; 扩展方式: b->a

        if( step <= MAX_STEP )  return step; //成功相遇
    }

    return MAX_STEP + 1;
}

int main()
{
    string A, B;
    cin >> A >> B;
    while( cin >> a[n] >> b[n] )    n ++;

    int step = bfs(A, B);
    if( step > MAX_STEP )   cout << "NO ANSWER!" << endl;
    else    cout << step << endl;

    return 0;
}