算法提高课汇总

算法思路

建图

首先考虑建图: 网格格点作为图中顶点, 电子元件作为边: 如果对角线格点不需要转动对应电子元件,
对应边的权值为0, 若需要转动电子元件, 对应边的权值为1.

上述建图方式成立需要路径满足: 同一个元件只会经过其一种状态: 转动或不转动.

即对一个元件, 不存在如下路径:

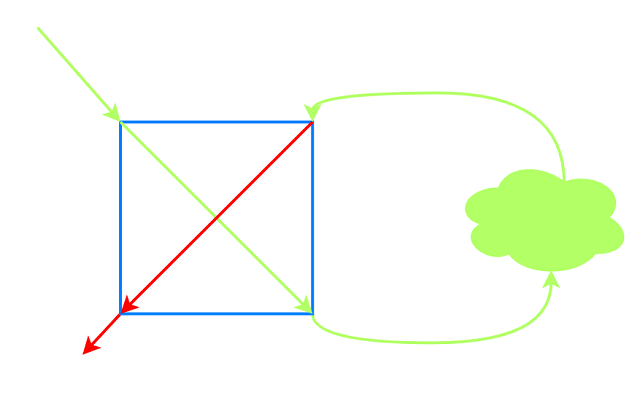
由于本题的性质(路径只会经过偶点), 上述路径不可能存在. 首先引入奇点和偶点的概念:

• 奇点/偶点: 网格点横纵坐标之和($i + j$)为奇数/偶数.

由于所有边均是对角线, 横纵坐标的奇偶性同时改变, 所以它们和的奇偶性保持不变.

若横纵坐标均从0开始, 则起点为偶点, 所以从起点出发的任何路径只会经过偶点. 而同一元件的
$4$个顶点只有一对对角点为偶点, 所以每个元件只会保持一种状态.

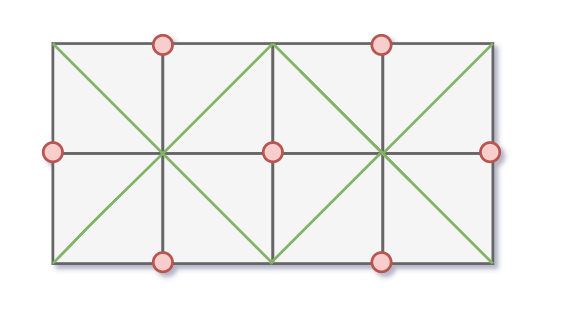
双端队列

建图后, 题目转变为边权为$0$/$1$的最短路问题. 可用双端队列$BFS$求解.

双端队列支持从对头插入和从队尾取出元素的操作, 在算法过程中:

• 每次取出对头节点$u$, 加入$u$相邻且未遍历顶点$v$, 若边权$w(u, v) = 0$, 则将$v$加入队头, 否则加入队尾.

这样操作的目的在于保持队列的两段性和单调性, 可用归纳法证明. 参考 AcWing 173. 矩阵距离
证明$BFS$正确性思路: 证明队列的两段性和单调性后, 算法等价于$Dijkstra$算法.

相比于普通$BFS$, 双端队列$BFS$更接近$Dijkstra$: 顶点出队时才能确定其全局最小值.

• 由于边权存在0, 对于顶点$v$, 在队列中$u$首先更新$d(v) = d(u) + 1$, 后续节点$d(u’) = d(u) + [1]$,
  其中+1可能存在可能不存在. 若此时$w(u’, v) = 0$, 用$u’$更新$v$的距离为$d(v) = d(u’)\le d(u) + 1$.

具体实现

• 双端队列可使用STL中的deque实现.

• 出队时才能确定顶点全局最小值, 所以顶点可能会多次入队. 类似$Dijkstra$, 用判重数组标记
  某顶点是否已经出队, 以降低运行时间.

• 注意格点和元件坐标的差异.

实现代码

#include <deque>
#include <cstring>
#include <iostream>

#define x first
#define y second

using namespace std;

typedef pair<int, int> pii;

const int N = 510;

int  n, m;
char g[N][N];
int  dist[N][N]; bool st[N][N]; pii q[N * N]; //bfs 由于可能多次入队, 用st判重

int bfs()
{
    char path[] = "\\/\\/";
    int dx[] = {-1, -1, 1, 1}, dy[] = {-1, 1, 1, -1}; //格点和相邻4个方向格点的坐标差
    int ix[] = {-1, -1, 0, 0}, iy[] = {-1, 0, 0, -1}; //格点和4个方向元件的坐标差

    memset(st, 0, sizeof st);
    memset(dist, 0x3f, sizeof dist);
    dist[0][0] = 0;
    deque<pii> que; 
    que.push_front({0, 0});

    while( que.size() )
    {
        pii cur = que.front(); que.pop_front();
        int x = cur.x, y = cur.y;

        if( x == n && y == m )  return dist[x][y]; //出队 到达终点

        if( st[x][y] )  continue; //由于可能多次入队 类似dijkstra
        st[x][y] = true; 

        for( int i = 0; i < 4; i ++ )
        {
            int nx = x + dx[i], ny = y + dy[i];
            int gx = x + ix[i], gy = y + iy[i];
            if( nx < 0 || nx > n || ny < 0 || ny > m )  continue; //注意格点下标范围比元件多1
            if( st[nx][ny] )    continue; //最小值已确定
            int w = g[gx][gy] != path[i];
            if( dist[nx][ny] > dist[x][y] + w )
            {
                dist[nx][ny] = dist[x][y] + w;
                if( w ) que.push_back({nx, ny});
                else    que.push_front({nx, ny});
            }
        }
    }
}

int main()
{
    int T;
    cin >> T;
    while( T -- )
    {
        cin >> n >> m;
        for( int i = 0; i < n; i ++ )   cin >> g[i];

        if( (n + m) & 1 )   cout << "NO SOLUTION" << endl; //目标点为奇点 不可能到达
        else    cout << bfs() << endl;
    }
    return 0;
}