题目描述

略

样例

略

算法

(思维) $O(6^2*4)$

这题其实还算比较好想的，只不过要把细节想明白还是挺麻烦的，写起来倒是也比立体推箱子1简单多了，仔细观察，我们会发现，要达到终点，必须得经过(x,y,0)且x%3==0,y%3==0的点，我们就称这样的点为模三点吧。

所以问题得转化成我们得从当前状态点转移到一个模三点，其次我们得考虑，要从一个模三点如何转移到相邻的一个模三点并且花费的代价最小，显然最小距离最少是2(这里可以画图试一试),归纳一下，从一个模三点转移到任意一个模三点最少代价，其实就是哈密顿距离/3*2，所以问题就转化为了，从当前位置找与他相邻的模三点的代价加上从这个模三点转移到原点的最小代价。

为什么要找与他相邻的呢？我们可以先画一个图。

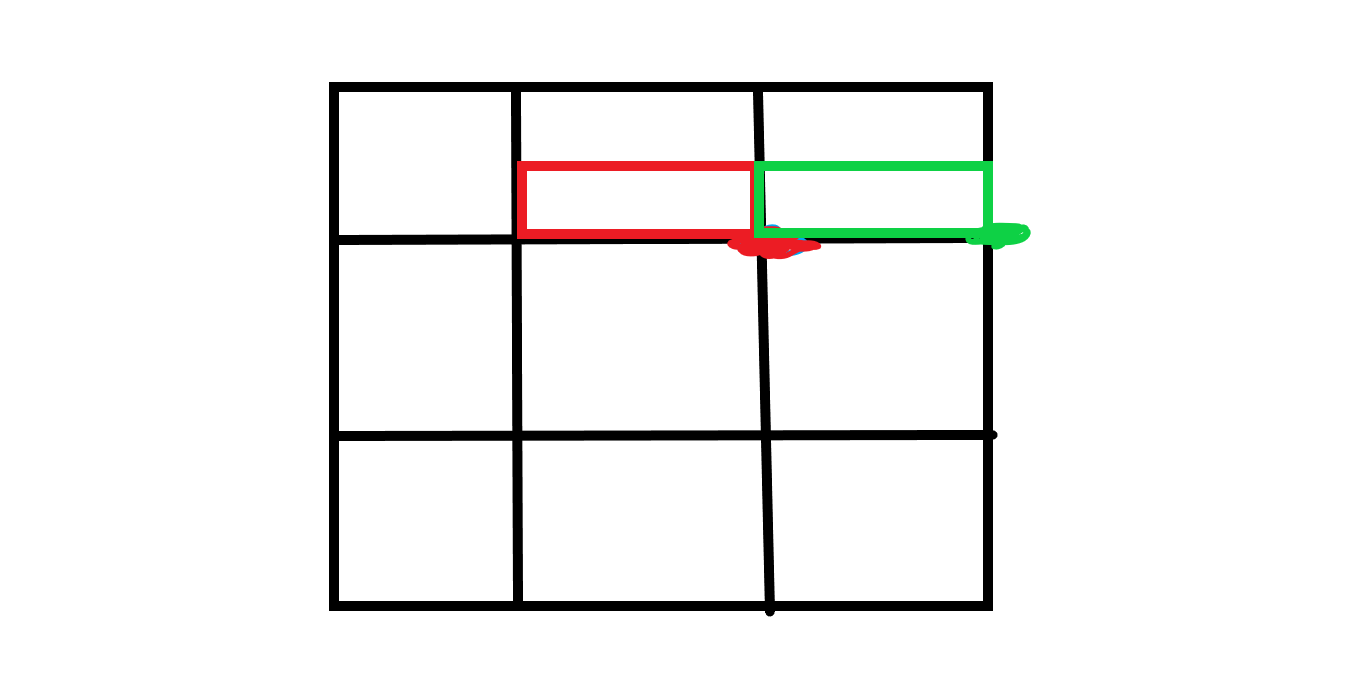
(图有点丑见谅)

每个方格代表3*3的矩阵，假设红色方框代表箱子当前的位置，它处在的是一个非模三位置，红点是与他相邻的一个模三点，那有没有必要转移到绿点这个‘不相邻’的模三点呢，我们可以发现，绿色方框转移到绿点和红色方框转移到红点是等价的，红点到绿点需要2的代价，而红色方框转移方框又需要不小于2的代价，所以没必要再转移到绿点。

这样我们只需要一个包含当前方格点在内的6^2的矩阵，就可以把(1e9)^2的矩阵缩小到6^2,这样直接BFS，判断当前点是不是模三点，更新最小值即可

当然这题还有一点需要注意的是坐标无限的，所以我们得把终点坐标平移到(3,3)，这里的处理稍微的注意下，我为此WA了几发…

本人ACwing第一篇题解，如有讲错的地方，请指出，蒟蒻一定改正!
下面附下代码

时间复杂度

6^2*4

C++ 代码

#include <iostream>
#include <cstring>
#include <queue>
#include <cstdio>
using namespace std;

struct node{
    int x,y,dir;
};

int dist[7][7][4];

bool check(int a,int b){
    return a>=0&&a<=6&&b>=0&&b<=6;
}

int bfs(node start,int pastx,int pasty){

    int res = 2e9;

    queue<node> q;
    q.push(start);
    memset(dist,0x3f,sizeof dist);
    dist[start.x][start.y][start.dir] = 0;

    int d[3][4][3] = {
        {{-2, 0, 2}, {0, 1, 1}, {1, 0, 2}, {0, -2, 1}},
        {{-1, 0, 1}, {0, 2, 0}, {1, 0, 1}, {0, -1, 0}},
        {{-1, 0, 0}, {0, 1, 2}, {2, 0, 0}, {0, -1, 2}}
    };

    while(q.size()){
        auto t = q.front();
        q.pop();

        if((t.x)%3==0&&(t.y)%3==0&&(t.dir)==0){
            int bnsx = ((t.x-3)+pastx)/3*2;
            int bnsy = ((t.y-3)+pasty)/3*2;
            if(bnsx<0||bnsy<0) continue;
            res = min(res,dist[t.x][t.y][0]+bnsx+bnsy);
        }
        for(int i=0;i<4;++i){
            int x = (t.x)+d[t.dir][i][0];
            int y = (t.y)+d[t.dir][i][1];
            int dir = d[t.dir][i][2];

            if(!check(x,y)) continue;
            if(dir==1&&!check(x,y+1)) continue;
            if(dir==2&&!check(x+1,y)) continue;

            if(dist[x][y][dir]==0x3f3f3f3f){
                dist[x][y][dir] = dist[t.x][t.y][t.dir]+1;
                q.push({x,y,dir});
            }
        }

    }
    return res;
}

int main(){
    char ch;
    int x,y;
    while(cin>>ch>>x>>y){
        int dir;
        if(ch=='H') dir = 1;
        else if(ch=='U') dir = 0;
        else dir = 2;
        node start = {x%3+3,y%3+3,dir};
        x-=x%3;
        y-=y%3;
        printf("%d\n",bfs(start,x,y));
    }
    return 0;
}