算法分析

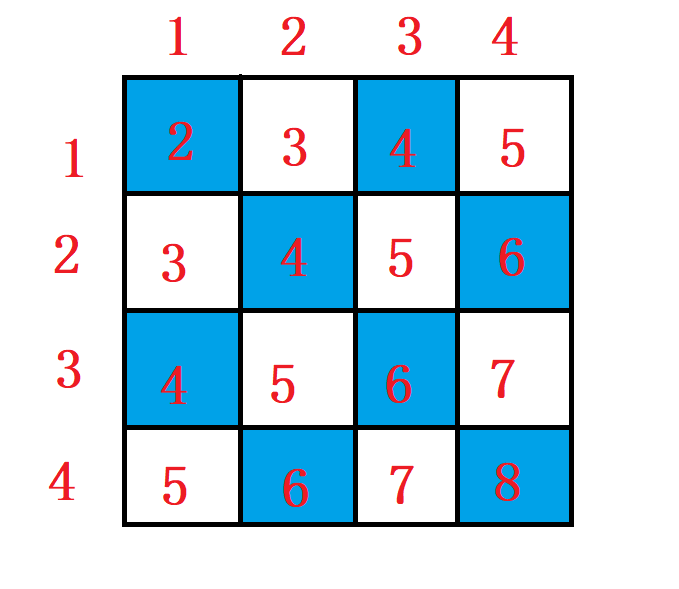
• 由于每个骨牌只会由连续的两个方块进行搭配，在方块的坐标的行列之和中，一定是偶数和奇数的搭配，即在图中每个蓝色方块只会和周围的白色方块组成一个骨牌，每一个白色方块只会和周围的蓝色方块组成一个骨牌，求组合的最大数，因此题目求的是一个二分图的最大匹配问题

• 只需求所有偶数方块的最大匹配之和即可，即偶数方块向奇数方块连一条有向边

时间复杂度 $O(n^4)$

参考文献

算法提高课

Java 代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int N = 110;
    static int n,m;
    static boolean[][] g = new boolean[N][N];//该位置不能踩
    static boolean[][] st = new boolean[N][N];
    static int[] dx = new int[] {-1,0,1,0};
    static int[] dy = new int[] {0,1,0,-1};
    static Pair[][] match = new Pair[N][N];
    static boolean find(int x,int y)
    {
        for(int i = 0;i < 4;i ++)
        {
            int a = x + dx[i];
            int b = y + dy[i];
            if(a <= 0 || a > n || b <= 0 || b > n) continue;
            if(st[a][b] || g[a][b]) continue;
            st[a][b] = true;
            Pair t = match[a][b];
            if(t.x == 0 || find(t.x,t.y))
            {
                t.x = x;
                t.y = y;
                return true;
            }
        }
        return false;
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        m = scan.nextInt();
        while(m -- > 0)
        {
            int x = scan.nextInt();
            int y = scan.nextInt();
            g[x][y] = true;
        }
        for(int i = 1;i <= n;i ++)
            for(int j = 1;j <= n;j ++)
                match[i][j] = new Pair(0,0);

        int res = 0;
        for(int i = 1;i <= n;i ++)
            for(int j = 1;j <= n;j ++)
            {   //只需求所有偶数方块的最大匹配之和即可
                if((i + j) % 2 == 0 && !g[i][j])
                {
                    for(int k = 1;k <= n;k ++) Arrays.fill(st[k], false);
                    if(find(i,j)) res ++;
                }
            }

        System.out.println(res);

    }
}
class Pair
{
    int x;
    int y;
    Pair(int x,int y)
    {
        this.x = x;
        this.y = y;
    }
}