题目描述

维护一个集合，支持如下几种操作：

“I x”，插入一个数x；
“Q x”，询问数x是否在集合中出现过；
现在要进行N次操作，对于每个询问操作输出对应的结果。

输入格式
第一行包含整数N，表示操作数量。

接下来N行，每行包含一个操作指令，操作指令为”I x”，”Q x”中的一种。

输出格式
对于每个询问指令“Q x”，输出一个询问结果，如果x在集合中出现过，则输出“Yes”，否则输出“No”。

每个结果占一行。

数据范围
1≤N≤105
−109≤x≤109

输入样例

5
I 1
I 2
I 3
Q 2
Q 5

输处样例

Yes
No

算法1

(线性试探法)

时间复杂度

参考文献

C++ 代码

#include <iostream>
#include <cstring>
using namespace std;

const int N = 2e5 + 3, nil = -1;
int h[N];

int key(int x) { // 线性试探法 保存的值容易扎堆
    int d = 1;   // 试探时偏移距离
    int t = (x % N + N) % N;  // 哈希函数
    while(h[t] != nil && h[t] != x) {  // 冲突
        if(t + d < N) t += d;          // 向元素h[t]的右边做线性试探       
        else if(t - d >= 0) t -= d;    // 向元素h[t]的左边做线性试探
        d++; // 试探失败，更新试探的偏移距离
    }
    return t;
}

void insert(int x) {
    h[key(x)] = x;
}

int find(int x) {
    // 映射到的值为空或映射到的值不为x则未命中 返回0
    if(h[key(x)] == nil || h[key(x)] != x) return 0;
    return 1;  // 否则命中 返回1
}

int main() {
    memset(h, nil, sizeof h); // 散列表初始化为空
    string s;
    int n, x;
    cin >> n;     
    while(n--) {
        cin >> s >> x;
        if(s == "I") insert(x);
        else if(s == "Q") find(x) ? puts("Yes") : puts("No");
    }
    return 0;
}

算法2

(平方试探法)

时间复杂度

参考文献

C++ 代码

#include <iostream>
#include <cstring>
using namespace std;

const int N = 2e5 + 3, nil = -1;
int h[N];

int key(int x) {  // 平方试探法 保存的值不易扎堆
    int d = 1;    // 试探时偏移距离的基数 
    int t = (x % N + N) % N; // 哈希函数  
    while(h[t] != nil && h[t] != x) {    // 冲突
        if(t + d << 1 < N) t += d << 1;  // 向元素h[t]的右边做平方试探
        else if(t - d << 1 >= 0) t -= d << 1; // 向元素h[t]的左边做平方试探
        d++;  // 试探失败，更新试探的距离基数
    }    
    return t;
} 

void insert(int x) {
    h[key(x)] = x;
}

int find(int x) {
    // 映射到的值为空或映射到的值不为x则未命中 返回0
    if(h[key(x)] == nil || h[key(x)] != x) return 0;
    return 1;  // 否则命中 返回1
}

int main() {
    memset(h, nil, sizeof h); // 散列表初始化为空
    string s;
    int n, x;
    cin >> n;     
    while(n--) {
        cin >> s >> x;
        if(s == "I") insert(x);
        else if(s == "Q") find(x) ? puts("Yes") : puts("No");
    }
    return 0;
}

算法3

(拉链法)

时间复杂度

参考文献

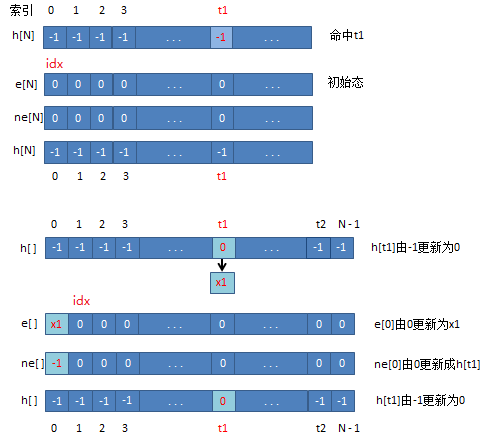
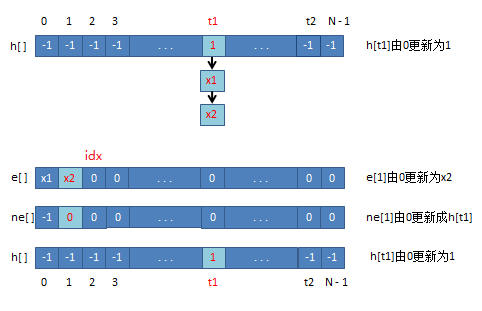
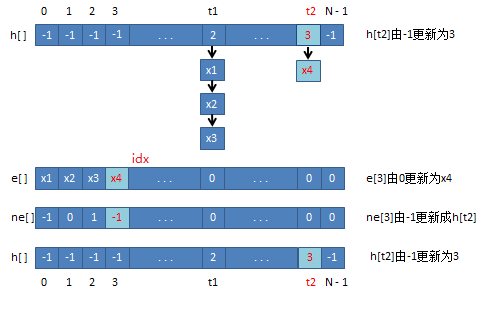
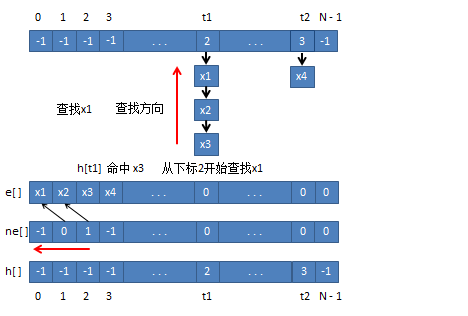
图示算法

C++ 代码

#include <cstring>
#include <iostream>
using namespace std;

const int N = 1e5 + 3, nil = -1; // nil 表示空
// 全局变量在堆中分配内存，且会自动初始化为0
// h[]散列表保存头节点的下标，为nil表示还未拉出链表
// e[]保存值，ne[]保存前一个值的下标，idx是链表的索引
int h[N], e[N], ne[N], idx; 

void insert(int x) {
    int t = (x % N + N) % N;
    e[idx] = x;      // 保存值
    ne[idx] = h[t];  // 保存头节点的下标，h[t]为nil链表的尾节点
    h[t] = idx++;    // 更新散列表中链表头节点的下标值，然后索引自增
}

// 每个链表都以nil作为结束的标记
int find(int x) {
    int t = (x % N + N) % N;
    // 如果多个数据的映射的结果相同，它们将被保存在同一根链表上
    // 先获取拉出的链表头结点，然后遍历直到命中或者全部不命中为止
    for(int i = h[t]; i != nil; i = ne[i])
       if(e[i] == x) return 1;   // 命中则返回1
    return 0;  // 全部都无法命中，返回0
}

int main() {
    memset(h, nil, sizeof h); // 散列表初始化为空
    string s;
    int n, x;
    cin >> n;
    while(n--) {
        cin >> s >> x;
        if(s == "I") insert(x);
        else if(s == "Q") find(x) ? puts("Yes") : puts("No");
    }
    return 0;
}