这道题目比较复杂,本来没有测试数据和标程的,在这里把自己写标程和添加测试数据的思路,以及遇到的坑点分享给大家。
首先是思路

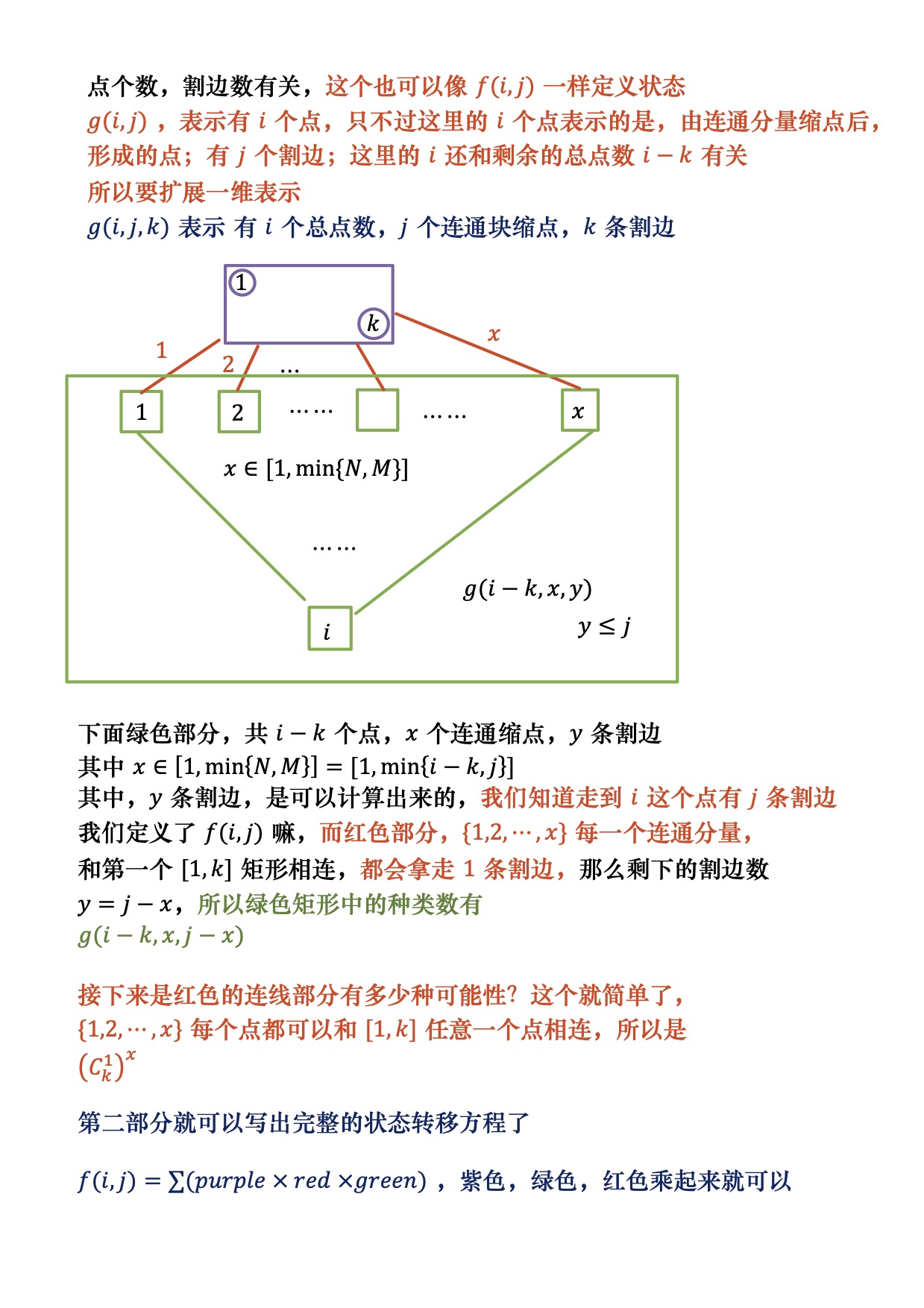

这道题目所预先处理的H[ ] ,可以参照
连通图
这是楼天成著名的男人八题。
接下来是代码部分,我遇到了一个问题就是,
这里我用了大整数类来直接打表计算。其实,想要程序代码简单一些的话,可以用费马大定理的乘法逆元来计算组合数。不过很神奇的是,我在windows的高配置台式机上跑, 逆元法求组合数,然后用 %mod 参与最终的计算,不会出问题 编译器是g++
但是我换到我的macbook中,同样的代码,会出现精度问题, 用的编译环境是xcode + clang
所以最后我用大整数类直接计算了
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <set>
#include <sstream>
#include <iomanip>
#include <cmath>
#include <bitset>
#include <assert.h>
using namespace std;
typedef long long ll;
typedef set<int>::iterator ssii;
#define Cmp(a, b) memcmp(a, b, sizeof(b))
#define Cpy(a, b) memcpy(a, b, sizeof(a))
#define Set(a, v) memset(a, v, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define _forS(i, l, r) for(set<int>::iterator i = (l); i != (r); i++)
#define _rep(i, l, r) for(int i = (l); i <= (r); i++)
#define _for(i, l, r) for(int i = (l); i < (r); i++)
#define _forDown(i, l, r) for(int i = (l); i >= r; i--)
#define debug_(ch, i) printf(#ch"[%d]: %d\n", i, ch[i])
#define debug_m(mp, p) printf(#mp"[%d]: %d\n", p->first, p->second)
#define debugS(str) cout << "dbg: " << str << endl;
#define debugArr(arr, x, y) _for(i, 0, x) { _for(j, 0, y) printf("%c", arr[i][j]); printf("\n"); }
#define _forPlus(i, l, d, r) for(int i = (l); i + d < (r); i++)
#define lowbit(i) (i & (-i))
#define MPR(a, b) make_pair(a, b)
// == Big Integer class ==
const int SZ = 200 + 5;
inline void write(ll x) {
if(x < 0) {
putchar('-');
x = -x;
}
if(x < 10) {
putchar(x + '0');
return;
}
write(x / 10);
putchar((x % 10) + '0');
}
const int base = 1e4;
class Int {
public:
int a[SZ], len;
Int() {
Set(a, 0);
len = 0;
}
Int(int x) {
Set(a, 0);
len = 0;
while (x) {
a[++len] = x % base;
x /= base;
}
}
inline void print() {
write(a[len]);
for(int i = len - 1; i; i--) {
if(a[i] < 1000) putchar('0');
if(a[i] < 100) putchar('0');
if(a[i] < 10) putchar('0');
write(a[i]);
}
}
};
inline Int operator+ (Int a, Int b) {
Int ans;
ans = a;
ans.len = max(a.len, b.len);
_rep(i, 1, ans.len) {
ans.a[i] += b.a[i];
ans.a[i + 1] += ans.a[i] / base;
ans.a[i] %= base;
}
while (ans.a[ans.len + 1]) ans.len++;
return ans;
}
inline Int operator / (Int a, int b) {
Int ans;
assert(ans.len == 0);
int num = 0;
for(int i = a.len; i; i--) {
num = num * base + a.a[i];
ans.a[i] = num / b;
num %= b;
if(ans.len == 0 && ans.a[i]) ans.len = i;
}
return ans;
}
inline ll operator % (Int a, int b) {
ll num = 0;
for(int i = a.len; i; i--) {
num = ((num * base) % b + a.a[i]) % b;
}
return num;
}
inline Int operator* (Int a, int b) {
Int ans = a;
_rep(i, 1, ans.len) ans.a[i] *= b;
_rep(i, 1, ans.len) {
ans.a[i + 1] += ans.a[i] / base;
ans.a[i] %= base;
}
while (ans.a[ans.len + 1]) {
ans.len++;
ans.a[ans.len + 1] += ans.a[ans.len] / base;
ans.a[ans.len] %= base;
}
return ans;
}
inline Int operator* (Int a, Int b) {
Int ans;
assert(ans.a[1] == 0);
ans.len = a.len + b.len;
_rep(i, 1, a.len) _rep(j, 1, b.len) {
ans.a[i+j-1] += a.a[i] * b.a[j];
ans.a[i+j] += ans.a[i+j-1] / base;
ans.a[i+j-1] %= base;
}
while (ans.a[ans.len] == 0) ans.len--;
return ans;
}
inline Int operator- (Int a, Int b) {
Int ans = a;
_rep(i, 1, b.len) {
ans.a[i] -= b.a[i];
if(ans.a[i] < 0) {
ans.a[i + 1]--;
ans.a[i] += base;
}
}
while (ans.a[ans.len] == 0) ans.len--;
return ans;
}
const int maxn = 50 + 2;
Int _c[maxn][maxn];
const int mod = 1e9 + 7;
ll H[maxn + 1];
// == table() and list H[] ==
const int Max = 1500;
Int bin[Max*2];
void initbin() {
bin[0] = Int(1);
_rep(i, 1, Max) bin[i] = bin[i - 1] * 2;
}
Int tb[maxn + 5];
void getH() {
initbin();
tb[1] = Int(1);
_rep(i, 2, maxn) {
tb[i] = bin[i*(i-1) / 2];
_for(j, 1, i) {
tb[i] = tb[i] - (tb[j] * _c[i-1][j-1] * bin[(i-j)*(i-j-1) / 2]);
}
}
}
void table() {
getH();
_rep(i, 1, maxn) H[i] = tb[i] % mod;
}
// == table() finsihed ==
const int maxm = 1250;
// == calculate C() ==
void initC() {
_c[0][0] = Int(1);
_rep(i, 1, maxn) {
_c[i][0] = Int(1);
_rep(j, 1, i) _c[i][j] = _c[i-1][j-1] + _c[i-1][j];
}
}
inline ll C(int n, int m) {
return _c[n][m] % mod;
}
ll power(ll a, int b) {
ll ans = 1;
for(; b; b >>= 1) {
if(b & 1) ans = ans * a % mod;
a = a * a % mod;
}
return ans;
}
// == C() finsihed, usage initC() and C(x, y) ==
// == first part, init f(i,j) ==
ll f[maxn][maxm];
ll sum[maxn][maxm];
void initf() {
Set(f, -1);
Set(sum, 0);
f[0][0] = 0;
f[1][0] = 1;
f[1][1] = 0;
f[2][0] = 0;
f[2][1] = 1;
f[2][2] = 0;
_for(i, 3, maxn) f[i][0] = 0;
}
// == f(i, j) finished ==
// == second part, init g(i,j,k) ==
ll g[maxn][maxn][maxm];
void initg() {
Set(g, -1);
_for(i, 0, maxn) _for(j, 0, maxm) g[0][i][j] = 0;
_for(k, 0, maxm) g[1][0][k] = 0;
g[1][1][0] = 1;
_for(k, 1, maxm) g[1][1][k] = 0;
//_for(i, 0, maxn) g[i][1][0] = 1;
g[2][1][1] = 2;
g[2][1][0] = 0;
//g[2][0][0] = 1;
//g[2][0][1] = 0;
}
// == g(i,j,k) finished ==
// == function G(i,j,k) ==
ll G(int i, int j, int k) {
if(g[i][j][k] >= 0) return g[i][j][k];
ll res = 0;
_rep(p, 1, i) _rep(q, 0, k) {
//debug(p);
//debug(q);
//debug(f[p][q]);
if(q >= p) continue;
assert(f[p][q] >= 0);
//debug(f[p][q]);
ll S = G(i-p, j-1, k-q);
assert(S >= 0);
res += (f[p][q] * C(i-1, p-1) % mod * p % mod * S) % mod;
res %= mod;
}
return g[i][j][k] = res;
}
// == G(i,j,k) finished ==
// == function cal(i, j, k) ==
ll cal(int i, int j, int k) {
assert(f[k][0] >= 0);
//debug(k), debug(f[k][0]);
//puts("");
//printf("i = %d, k = %d, %lld\n",i, k, C(i-1, k-1));
ll S1 = f[k][0] * C(i-1, k-1) % mod;
//debug(C(i-1, k-1));
ll S2 = 0;
_rep(x, 1, min(i-k, j)) {
S2 = (S2 + (G(i-k, x, j-x) * power(k, x)) % mod) % mod;
}
// if(i == 3) debug(S2);
return S1 * S2 % mod;
}
// == cal(i, j, k) finsihed ==
// == then solve ==
const int N = 50;
const int M = 1250;
void solve() {
_rep(i, 3, N) {
f[i][0] = H[i];
_for(j, 1, i) {
//assert(f[i][j] <= 0);
f[i][j] = 0;
_rep(k, 1, i - 1) {
f[i][j] = (f[i][j] + cal(i, j, k)) % mod;
}
f[i][0] = (f[i][0] - f[i][j] + mod) % mod;
}
}
}
// == solve finished ==
int main() {
//freopen("input.txt", "r", stdin);
freopen("sol.out", "w", stdout);
initC();
table();
initf();
initg();
solve();
//debug(H[52]);
//debug(H[3]);
//debug(f[3][1]);
//debug(f[3][2]);
debug(g[2][1][1]);
debug(g[2][1][0]);
_rep(i, 1, N) {
cout << i << ": ";
printf(" || H[i]=%lld || ", H[i]);
_rep(j, 0, 10) printf("%lld ", f[i][j]);
puts("");
}
cout << "\n===================\n" << endl;
// == get another table ==
_rep(i, 0, N) {
if(i == 0) {
_rep(j, 0, N) printf("0, ");
printf("\n");
continue;
}
_rep(j, 0, N) {
if(f[i][j] < 0) printf("0, ");
else printf("%lld, ", f[i][j]);
}
printf("\n");
}
// == table end ==
}


红色部分是用来干什么的啊
经过查找我发现您的标程 $g[3][1][2] = 0$,依照定义的话,3 个点,1一个联通块,2个割边是存在的呀,并且值为 9。
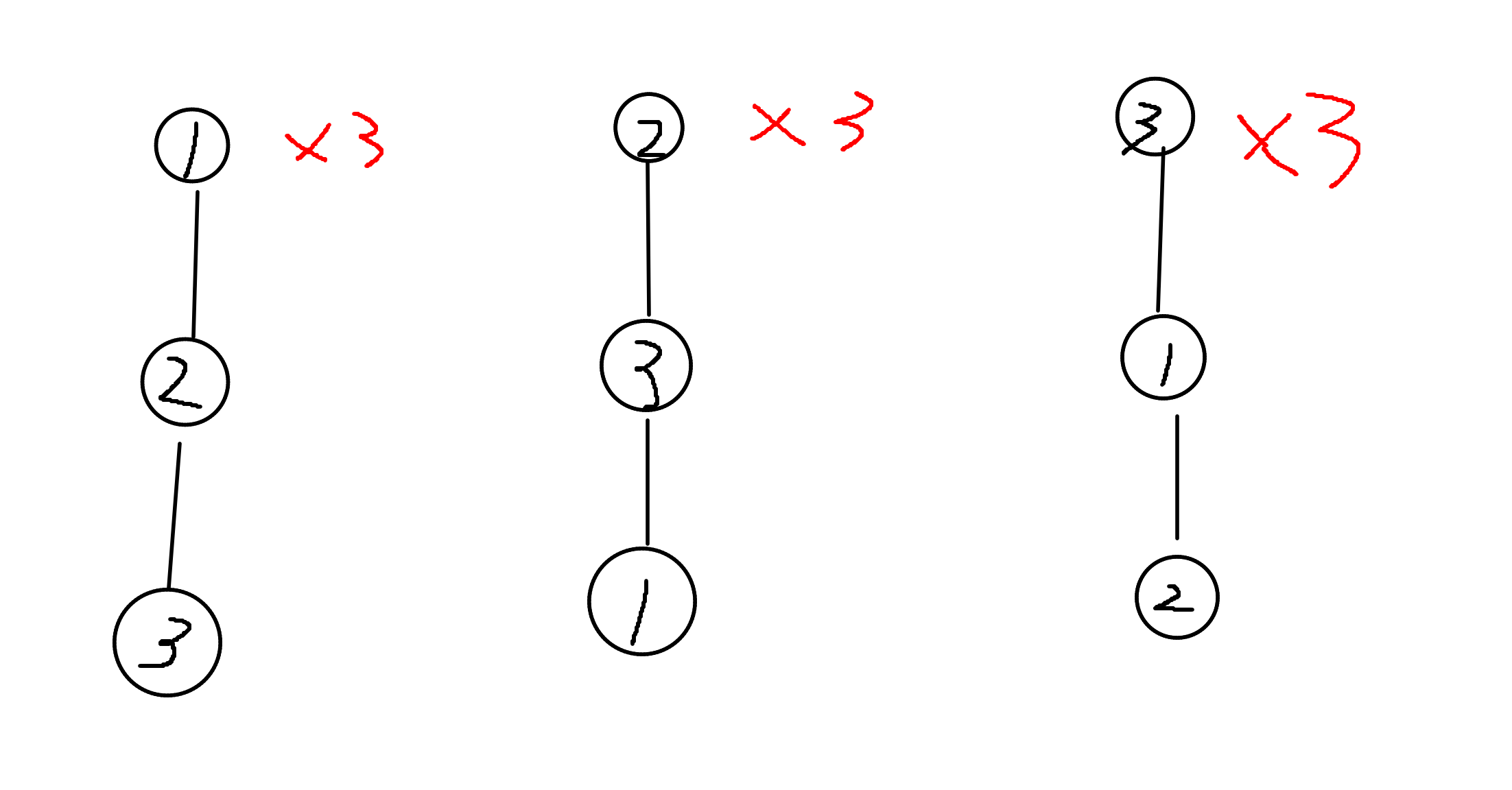
我寻找了我的程序与您不一样的地方。我发现lyd书上有个漏洞,就是在 $G$ 函数中,若 $j = 1$,我认为不应该直接转移由 $j = 0$ 转移来,这样就没有意义了,而是直接特判,因为 $G[i][1][k] = F[i][k] * i$。
麻烦您看一下这里
请问,为啥要 *i 呢?不太理解,求教~~
这里得初始化一下G(i, 1, k),我都忘了。。。
好长的题目和代码