算法分析

拓扑排序 + 虚拟点

题目描述：如果这趟车次停靠了火车站x，则始发站、终点站之间所有级别大于等于火车站x的都必须停靠

翻译过来：停靠过的车站的等级一定严格大于为停靠过的车站的等级，因此车站的等级均有严格的大小关系，则不存在环，因此可以用拓扑排序每个车站在图中的大小关系，使用动态规划求出车站等级最大的最小值(方法和 Acwing 1192奖金 类似)

在建边的时候，最坏情况下是有1000趟火车，每趟有1000个点，每趟上限有500个点停站，则有(1000 - 500)个点不停站，不停站的点都向停站的点连有向边，则总共有500 * 500 * 1000 = 2.5 * 10^8,则会超内存，如果用邻接矩阵存储，需要遍历所有的边，遍历的次数也是2.5 * 10^8，因此会超时，所以在每趟火车所有不停站的点向所有停站的点连有向边时，中间添加一个ver辅助结点，如下图连接方式

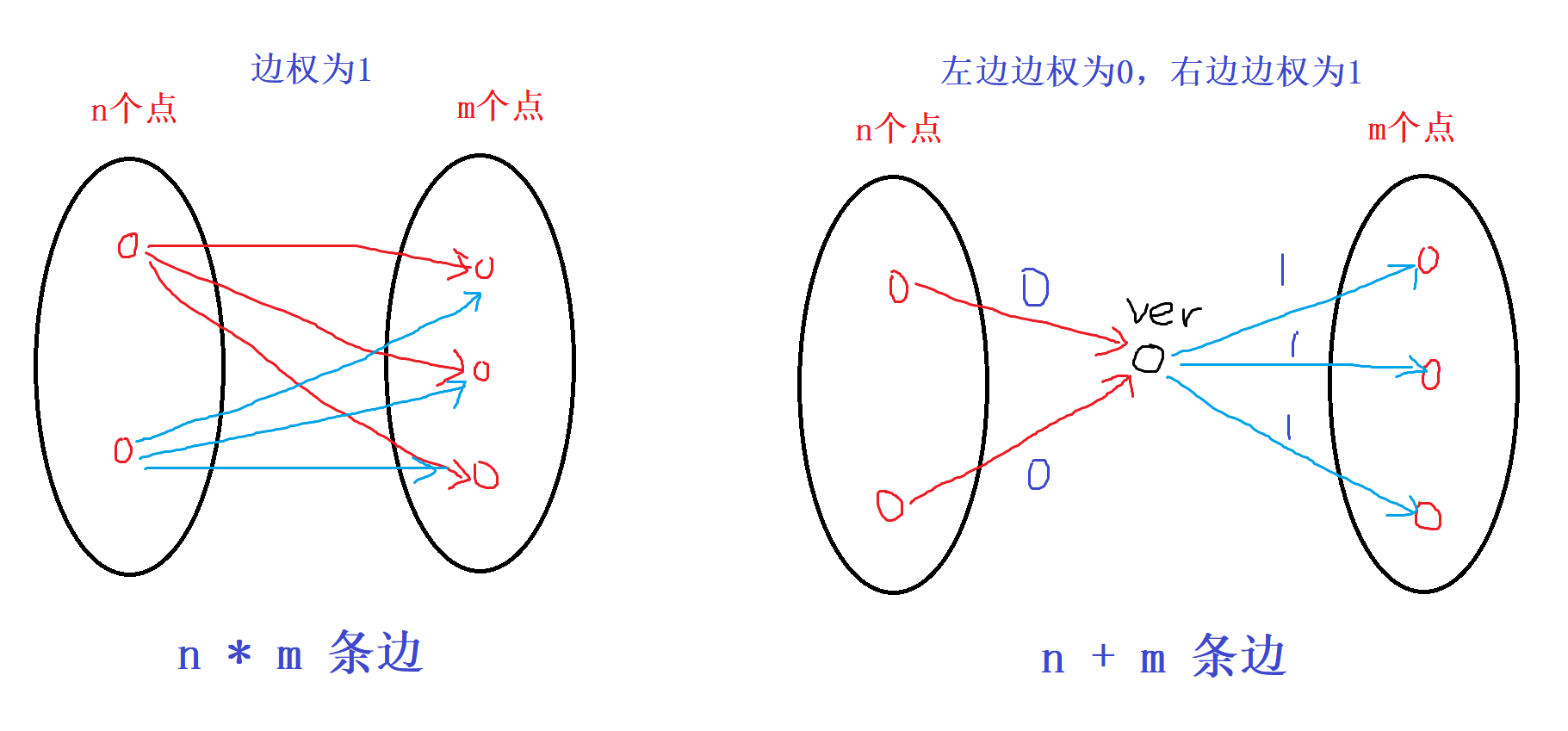
dist[i]：表示i点在拓扑图中离起点的最远距离(可能存在多起点)，dist[起点] == 1,边的权值为1

时间复杂度 $O(n + m)$

参考文献

算法提高课

Java 代码

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;

public class Main {
    static int N = 2010,M = 1000010;
    static int n;
    static int m;
    static int[] h = new int[N];
    static int[] e = new int[M];
    static int[] w = new int[M];
    static int[] ne = new int[M];
    static int idx = 0;
    static int[] d = new int[N];
    static int[] qv = new int[N];
    static int qidx = 0;
    static boolean[] st = new boolean[N];
    static int[] dist = new int[N];
    static void add(int a,int b,int c)
    {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx ++;
    }
    static void topsort()
    {
        Queue<Integer> q = new LinkedList<Integer>();
        for(int i = 1;i <= n + m;i ++)
        {
            if(d[i] == 0)
            {
                q.add(i);
                qv[qidx ++] = i;
            }
        }

        while(!q.isEmpty())
        {
            int t = q.poll();
            for(int i = h[t];i != -1;i = ne[i])
            {
                int j = e[i];
                if(-- d[j] == 0)
                {
                    q.add(j);
                    qv[qidx ++] = j;
                }
            }
        }
    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] s1 = br.readLine().split(" ");
        n = Integer.parseInt(s1[0]);
        m = Integer.parseInt(s1[1]);
        Arrays.fill(h, -1);
        for(int i = 1;i <= m;i ++)
        {
            String[] s2 = br.readLine().split(" ");
            Arrays.fill(st, false);
            int start = n,end = 1;
            for(int j = 1;j < s2.length;j ++)
            {
                int x = Integer.parseInt(s2[j]); 
                start = Math.min(start, x); 
                end = Math.max(end, x); 
                st[x] = true;
            }
            int ver = n + i;//虚拟结点
            for(int j = start;j <= end;j ++)
            {
                if(!st[j]) 
                {
                    add(j,ver,0);//该点向虚拟结点连一条权值为0的边
                    d[ver] ++;
                }
                else 
                {
                    add(ver,j,1);//虚拟结点向该点连一条权值为1的边
                    d[j] ++;
                }
            }
        }

        topsort();
        for(int i = 1;i <= n;i ++) dist[i] = 1;
        for(int i = 0;i < n + m;i ++)
        {
            int j = qv[i];
            for(int k = h[j];k != -1;k = ne[k])
            {
                int x = e[k];
                dist[x] = Math.max(dist[x], dist[j] + w[k]);
            }
        }
        int res = 0;
        for(int i = 1;i <= n;i ++) res = Math.max(res, dist[i]);
        System.out.println(res);
    }
}