题目描述

自从曹冲搞定了大象以后，曹操就开始琢磨让儿子干些事业，于是派他到中原养猪场养猪，可是曹冲很不高兴，于是在工作中马马虎虎，有一次曹操想知道母猪的数量，于是曹冲想狠狠耍曹操一把。

举个例子，假如有 16 头母猪，如果建了 3 个猪圈，剩下 1 头猪就没有地方安家了；如果建造了 5 个猪圈，但是仍然有 1 头猪没有地方去；如果建造了 7 个猪圈，还有 2 头没有地方去。

你作为曹总的私人秘书理所当然要将准确的猪数报给曹总，你该怎么办？

样例

输入格式
第一行包含一个整数 n，表示建立猪圈的次数；

接下来 n 行，每行两个整数 ai,bi，表示建立了 ai 个猪圈，有 bi 头猪没有去处。

你可以假定 ai,aj 互质。

输出格式
输出仅包含一个正整数，即为曹冲至少养猪的数目。

数据范围
1≤n≤10,
1≤bi≤ai≤1100000
所有ai的乘积不超过 1018
输入样例：
3
3 1
5 1
7 2
输出样例：
16

中国剩余定理裸题

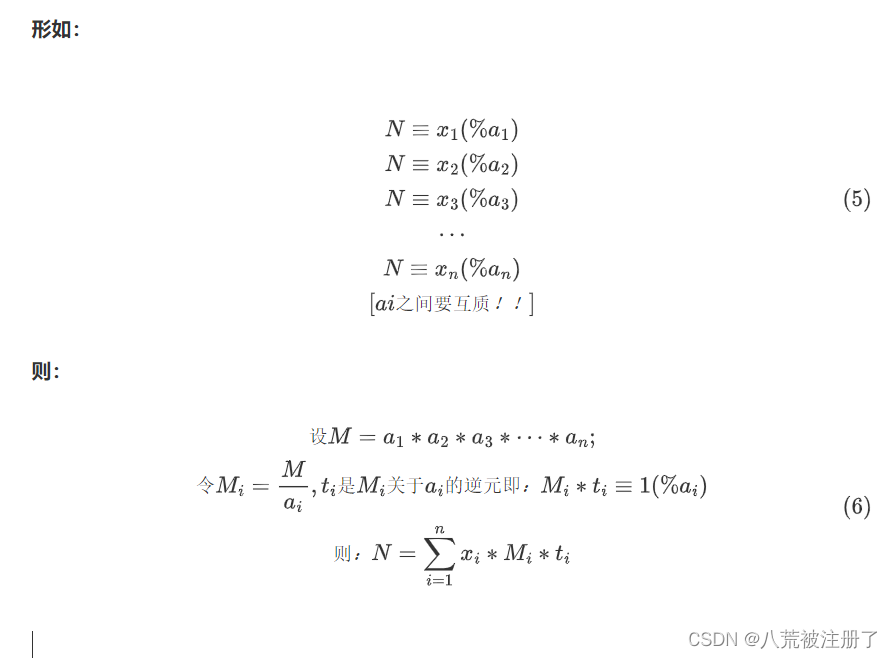
参考文献

提高课5.3

C++ 代码

/*
author: A Fei
solution: 同余方程组
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
typedef long long LL;
using namespace std;
int a[11], m[11];
int n;

LL exgcd(LL a, LL b, LL &x, LL &y)
{
    if(!b)
    {
        x = 1, y = 0;
        return a;
    }

    LL d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}
int main()
{
    scanf("%d", &n);

    LL M = 1;
    for(int i = 0; i < n; i ++) scanf("%d%d", &m[i], &a[i]), M *= m[i];

    LL res = 0;
    for(int i = 0; i < n; i ++)
    {
        LL mi = M/m[i];
        LL t, y;
        exgcd(mi, (LL)m[i], t, y);
        // t = (t % m[i] + m[i]) % m[i];
        res += (LL)a[i] * t * mi;
    }

    printf("%lld\n", (res % M + M) % M);//对于任意x+kM都是满足要求的解，但目标是输出最小的正整数x，因此取模即可

    return 0;
}