2022秋招备战！每天写至少一篇Leetcode里Hard难度题目的题解

2132. 用邮票贴满网格图

给你一个 m x n 的二进制矩阵 grid ，每个格子要么为 0 （空）要么为 1 （被占据）。

给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩阵中，且满足以下 限制 和 要求 ：

1. 覆盖所有 空 格子。
2. 不覆盖任何 被占据 的格子。
3. 我们可以放入任意数目的邮票。
4. 邮票可以相互有 重叠 部分。
5. 邮票不允许 旋转 。
6. 邮票必须完全在矩阵 内 。

如果在满足上述要求的前提下，可以放入邮票，请返回 true ，否则返回 false 。

示例 1：

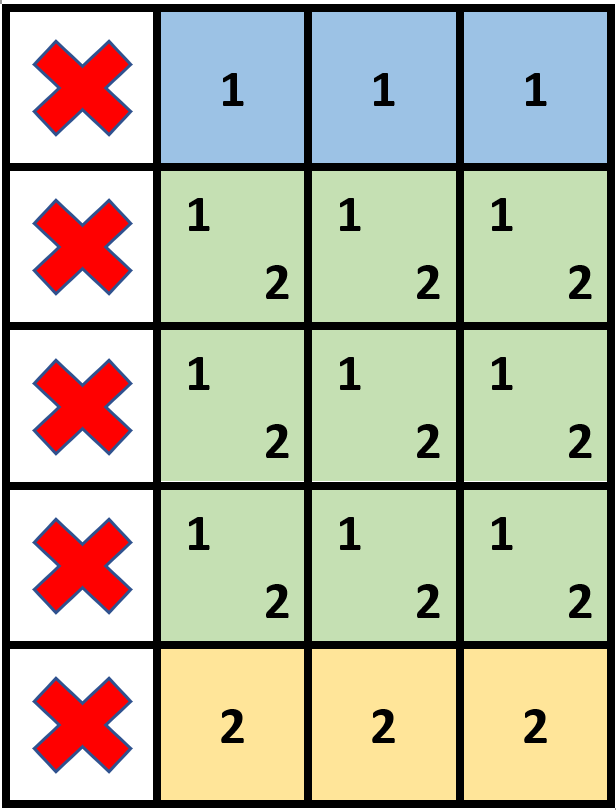
输入：grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3
输出：true
解释：我们放入两个有重叠部分的邮票（图中标号为 1 和 2），它们能覆盖所有与空格子。

示例 2：

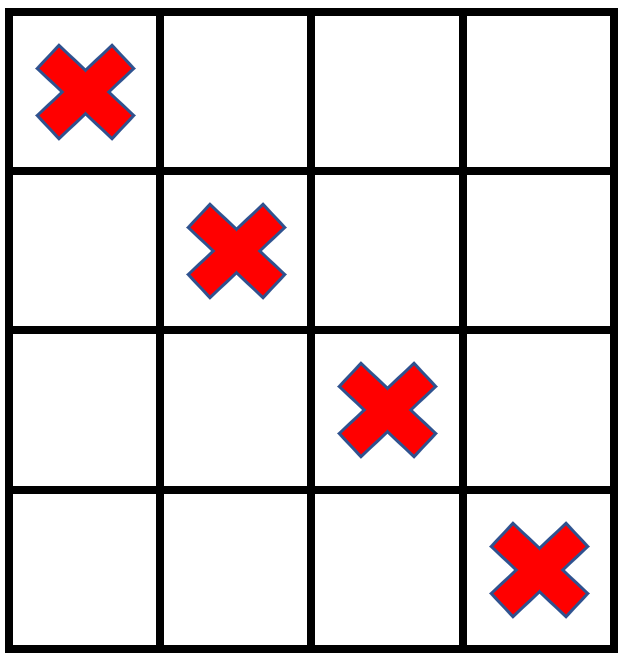
输入：grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 
输出：false 
解释：没办法放入邮票覆盖所有的空格子，且邮票不超出网格图以外。

提示：

• m == grid.length
• n == grid[r].length
• 1 <= m, n <= 105
• 1 <= m * n <= 2 * 105
• grid[r][c] 要么是 0 ，要么是 1 。
• 1 <= stampHeight, stampWidth <= 105

二维前缀和+二维差分

本题的思路其实非常暴力。

本题可以很好地复习基础课里二维前缀和和二维差分的内容。我在算法基础课上Y总的代码进行了小小的总结。

我们枚举网格里每一个位置，贪心地对能填充的地方进行填充。

如何验证该节点是否能填充，需要用到二维前缀和的思想。

对障碍物（为1的节点）进行前缀和的预处理，如果该邮票区域的二维前缀和大于1，说明无法填充，去枚举下一个点即可。

同时，我们用二维差分数组，记录重叠的邮票对原来的计数网格里的影响。

在最后还原我们的计数矩阵，对计数矩阵进行枚举即可。如果等于，说明没有被填充。

下面的代码不是最简洁的写法，但是很模式化，方便今后的ctrl + v。

class Solution {
public:
    bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> prefix(m + 1, vector<int>(n + 1)), diff(m + 10, vector<int>(n + 10));

        auto insert = [&](int x1, int y1, int x2, int y2, int c){
            diff[x1][y1] += c;
            diff[x2 + 1][y1] -= c;
            diff[x1][y2 + 1] -= c;
            diff[x2 + 1][y2 + 1] += c;
        };

        auto getSum = [&](int x1, int y1, int x2, int y2) {
            return prefix[x2][y2] - prefix[x1 - 1][y2] - prefix[x2][y1 - 1] + prefix[x1 - 1][y1 - 1];
        };

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (grid[i - 1][j - 1] > 0) insert(i, j, i , j, 1);
            }
        }

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                prefix[i][j] = prefix[i - 1][j] + prefix[i][j - 1] - prefix[i - 1][j - 1] + grid[i - 1][j - 1];
            }
        }
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                int r = i + stampHeight - 1, c = j + stampWidth - 1;
                if (r >= 0 && r <= m && c >= 0 && c <= n && getSum(i, j, r, c) == 0) {
                    insert(i, j , r, c, 1);
                }
            }
        }
        //把差分数组更新成前缀和数组

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                diff[i][j] += diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1];
            }
        }

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (diff[i][j] == 0) return false;
            }
        }
        return true;
    }
};