算法提高课汇总

算法思路

判断某些点构成的子图是否是半联通子图:

• 若点均属于某个强联通分量, 则一定可以构成半联通子图.

• 对任意两点$u, v$存在$u\rightarrow v$或$v\rightarrow u$.

综合两点, 考虑对原图缩点后的$DAG$:

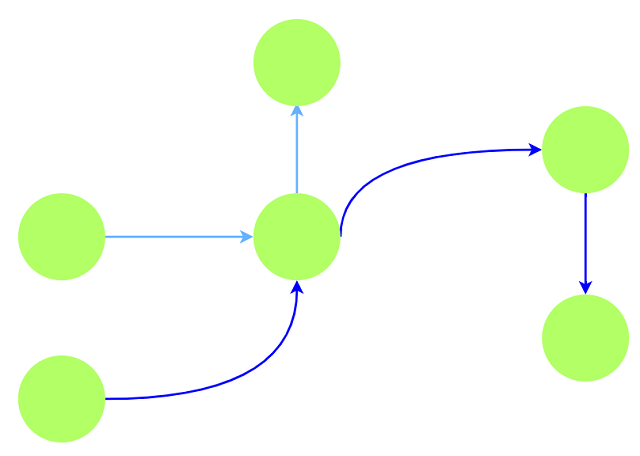
任意一条路径上的所有顶点构成的子图均可构成半联通子图: 点内为强联通分量,
点之间按拓扑序一定存在$u\rightarrow v$.

问题转化为求$DAG$上最长路径的权值(以每个强连通分量节点数目为权重)以及最长路径的数目.

具体实现

• 定义状态$f(u)$/$g(u)$: 以$u$为终点路径权值的最大/对应最大值的方案数.

• 最优解方案数思路可参考 连接🔗 .

• 注意不同强连通分量间不能有重边, 否则方案数会重复计数. 实际上按照定义若选择强联通分量$u, v$,
  则$u, v$间的所有边均在$G’$内, 只有这一种情况, 所以我们只考虑一次.

实现代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <unordered_set>

using namespace std;

typedef long long ll;

const int N = 1e5 + 10, M = 2e6 + 10;

int n, m, mod;
int h[N], hs[N], e[M], ne[M], idx; //hs: 缩点后的DAG
int dfn[N], low[N], timestamp;
int stk[N], top; bool in_stk[N];
int id[N], cize[N], scc_cnt;
int f[N], g[N];

void add(int h[], int u, int v)
{
    e[idx] = v, ne[idx] = h[u], h[u] = idx ++ ;
}

ll get_hash(int a, int b)
{//将(a, b) --> 不重复值
    return a * (ll)N + b; //(a, b) --> a0..0b
}

void tarjan(int u)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[++ top] = u, in_stk[u] = true;

    for( int i = h[u]; ~i; i = ne[i] )
    {
        int v = e[i];
        if( !dfn[v] )
        {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if( in_stk[v] )
        {
            low[u] = min(low[u], low[v]);
        }
    }

    if( dfn[u] == low[u] )
    {
        ++ scc_cnt;
        int v;
        do {
            v = stk[top --];
            in_stk[v] = false;
            id[v] = scc_cnt;
            cize[scc_cnt] ++;
        }while ( u != v );
    }
}

int main()
{
    scanf("%d%d%d", &n, &m, &mod);
    memset(h, -1, sizeof h);
    while( m -- )
    {
        int u, v;
        scanf("%d%d", &u, &v);
        add(h, u, v);
    }

    for( int u = 1; u <= n; u ++ )
        if( !dfn[u] )
            tarjan(u);

    //缩点操作 建立DAG
    memset(hs, -1, sizeof hs);
    unordered_set<ll> S;
    for( int u = 1; u <= n; u ++ )
        for( int i = h[u]; ~i; i = ne[i] )
        {
            int v = e[i];
            if( id[u] != id[v] )
            {
                ll hash = get_hash(id[u], id[v]);
                if( !S.count(hash) )
                {
                    S.insert(hash);
                    add(hs, id[u], id[v]);
                }
            }
        }

    //按拓扑序更新f[], g[]
    for( int u = scc_cnt; u; u -- )
    {
        if( !f[u] )
        {//起点
            f[u] = cize[u];
            g[u] = 1;
        }
        for( int i = hs[u]; ~i; i = ne[i] )
        {
            int v = e[i];
            if( f[v] < f[u] + cize[v] )
            {
                f[v] = f[u] + cize[v];
                g[v] = g[u];
            }
            else if( f[v] == f[u] + cize[v] )
                g[v] = (g[v] + g[u]) % mod;
        }
    }

    int max_f = 0, sum = 0;
    for( int u = 1; u <= scc_cnt; u ++ )
    {
        if( max_f < f[u] )
        {
            max_f = f[u];
            sum = g[u];
        }
        else if( max_f == f[u] )
            sum = (sum + g[u]) % mod;
    }
    printf("%d\n%d\n", max_f, sum);

    return 0;
}