算法提高课汇总

模型抽象

由于我们可以通过$tarjan$求强连通分量使得原图 --> $DAG$, 下面只考虑拓扑图.

Q1

首先考虑第一问, 假设拓扑图如下(设有$P$个起点, $Q$个终点):

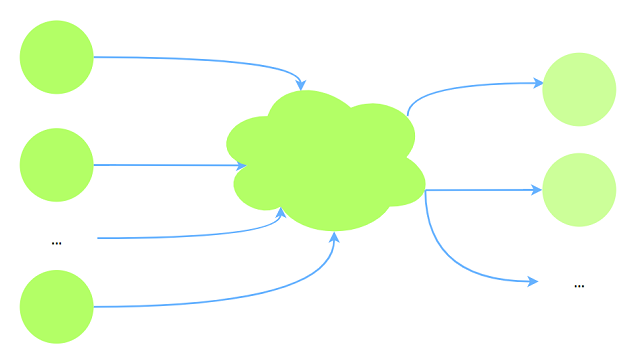
假设答案个数为$res$:

• $res\ge Q$: 显然每个起点都需要软件.

• $res = Q$: 可以认为建立虚拟起点指向所有起点, 从虚拟源点出发按拓扑序可以到达所有后继节点.

所以第一问答案为起点个数.

Q2

在原图中至少增加几条边 --> 强连通图.

对于本题起点和终点是对称的: 考虑加入$ans$条边, 如果此时我们将所有边反向(包括加入的新边),
起点和终点互换, 对结果没有影响. 所以下面只考虑$P\le Q$的情况.

只有1个节点

或者说原图只有一个强联通分量, 则已经满足条件, 不需要增加有向边.

$P = 1$

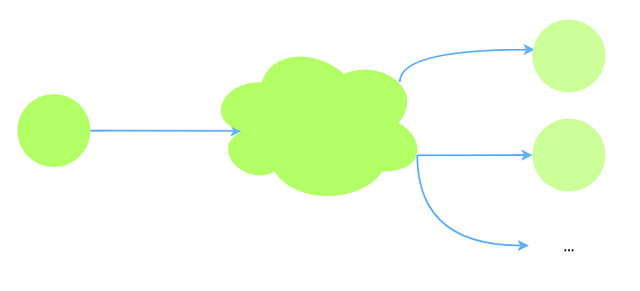
只有一个起点, 假设至少加$ans$条边:

• $ans\ge Q$: 软件传递过程到终点为止, 对每个终点都需要再传递给其他点.

• $ans = Q$: 将所有终点向起点连一条有向边即可.

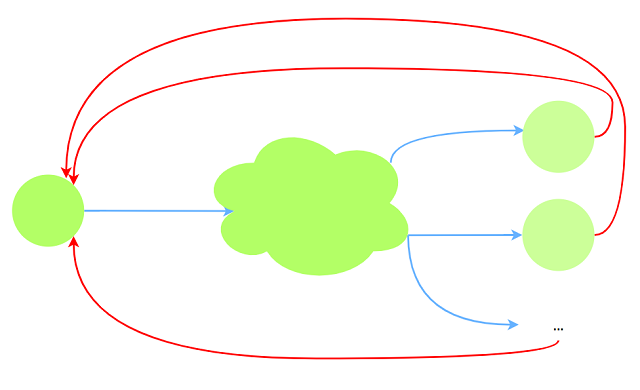
$P\gt 1$

有多个起点, 假设至少加$ans$条边, $ans\ge Q$. 考虑一种将终点软件传递给其他节点方式:
每次从一个终点向任意一个起点连一条边.

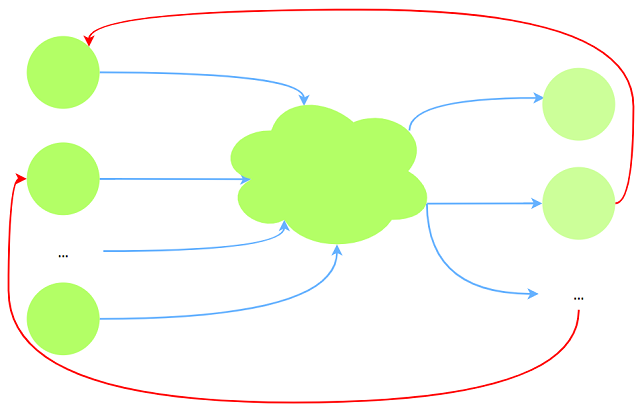
经过每次操作, 起点个数和终点个数均减1. 由于$P\le Q$, 当操作$P - 1$次后, 只剩下$1$个起点,
$Q - (P - 1)$个终点. 此时问题形式转变为$P = 1$, 所以$ans = P - 1 + Q - (P - 1) = Q$.

若此时$P\ge Q$, 我们将所有边反向, 则起点和终点互换, $ans = P$. 也就是问题结果是$max(P, Q)$.

代码实现 $O(V + E)$

#include <cstring>
#include <iostream>

using namespace std;

const int N = 110, M = N * N;

int n;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top; bool in_stk[N];
int id[N], scc_cnt;
int din[N], dout[N]; //起点和终点个数

void add(int u, int v)
{
    e[idx] = v, ne[idx] = h[u], h[u] = idx ++;
}

void tarjan(int u)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[++ top] = u; in_stk[u] = true;

    for( int i = h[u]; ~i; i = ne[i] )
    {
        int v = e[i];
        if( !dfn[v] )
        {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if( in_stk[v] )
        {
            low[u] = min(low[u], low[v]);
        }
    }

    if( dfn[u] == low[u] )
    {
        scc_cnt ++;
        int v;
        do {
            v = stk[top --];
            in_stk[v] = false;
            id[v] = scc_cnt;
        }while( u != v );
    }
}

int main()
{
    cin >> n;
    memset(h, -1, sizeof h);
    for( int u = 1; u <= n; u ++ )
    {
        int v;
        while( cin >> v, v )    add(u, v);
    }

    for( int u = 1; u <= n; u ++ )
        if( !dfn[u] )
            tarjan(u);

    for( int u = 1; u <= n; u ++ )
    {//缩点
        for( int i = h[u]; ~i; i = ne[i] )
        {
            int v = e[i];
            if( id[u] != id[v] )
            {
                dout[ id[u] ] ++ ; din[ id[v] ] ++ ;
            }
        }
    }

    int in_cnt = 0, out_cnt = 0; //起点、终点个数
    for( int i = 1; i <= scc_cnt; i ++ )
    {
        if( !din[i] )   in_cnt ++;
        if( !dout[i] )  out_cnt ++;
    }
    cout << in_cnt << endl;
    if( scc_cnt == 1 )  cout << 0 << endl;
    else    cout << max(in_cnt, out_cnt) << endl;

    return 0;
}