算法提高课汇总

理解题意

一头🐂受其他所有🐂欢迎: 从其他点出发均可到达该🐂.

可以反向建边, 若从某头牛出发可以到达其他所有🐂, 则该点满足条件. 若用$bfs$实现,
需要时间$O(V\times (V + E))$.

$Tarjan$求强连通分量

$DAG$简化问题

考虑一种简单情况: 原图是拓扑图. 可分为两种情况: 拓扑图只有1个终点; 有大于1个终点.

如果拓扑图中存在大于1个终点, 由于终点互相不可达, 则不存在一个🐂受其他所有牛欢迎.

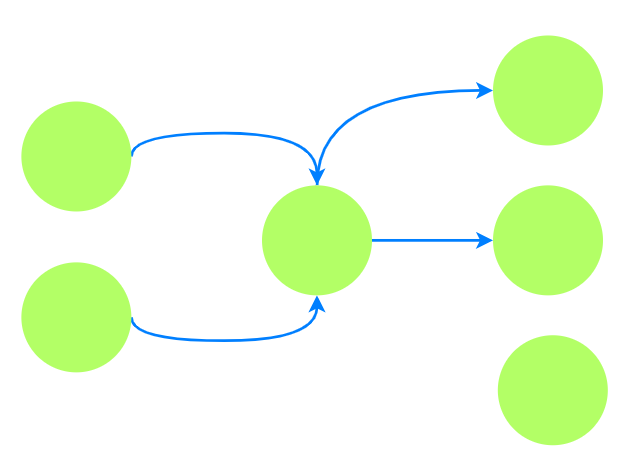
如果拓扑图只存在1个终点, 则终点即是受其他所有牛欢迎的🐂.

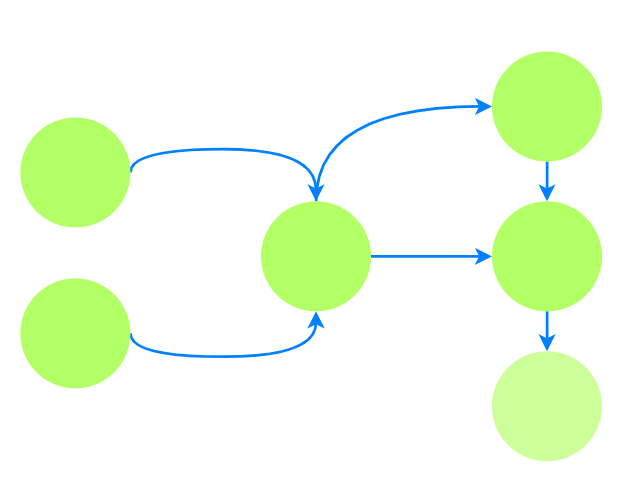
$Tarjan$强连通分量

对于较为复杂的有环图结构, 可以通过$tarjan$求强连通分量, 并将强连通分量视为一个节点. 则问题
转变为$DAG$上的问题. 关于$tarjan$求强连通分量可参考有向图的强连通分量 .

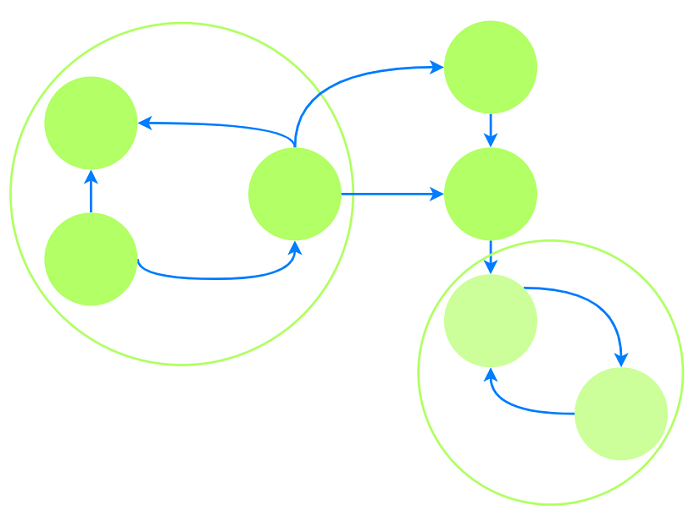
如果只有一个强连通分量作为终点: 分量内的顶点互相可以到达, 分量外的顶点可以到达分量, 则
该强连通分量内所有顶点均满足条件.

$Tarjan$与拓扑序

在通过$Tarjan$算法与缩点操作将原图 --> 拓扑图后, 不需要再对拓扑图进行拓扑排序. 因为$tarjan$算法
访问强联通分量顺序与$dfs$求拓扑序访问节点顺序相同; 拓扑序为得到强连通分量顺序的逆序.

对于本题实际上我们只关注拓扑序终点信息, 只需要记录节点出度即可.

具体实现

代码实现 $O(V + E)$

#include <cstring>
#include <iostream>

using namespace std;

const int N = 1e4 + 10, M = 5e4 + 10;

int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp; //记录时间戳
int stk[N], top; bool in_stk[N]; //栈
int id[N], scc_cnt, cize[N]; //强连通分量序号 大小
int dout[N]; //强联通分量出度

void add(int u, int v)
{
    e[idx] = v, ne[idx] = h[u], h[u] = idx ++;
}

void tarjan(int u)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[++ top] = u; in_stk[u] = true;

    for( int i = h[u]; ~i; i = ne[i] )
    {
        int v = e[i];
        if( !dfn[v] )
        {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if( in_stk[v] )
        {
            low[u] = min(low[u], low[v]);
        }
    }

    if( dfn[u] == low[u] )
    {
        scc_cnt ++;
        int v;
        do{
            v = stk[top --];
            in_stk[v] = false;
            id[v] = scc_cnt;
            cize[scc_cnt] ++;
        }while( u != v );
    }
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    while( m -- )
    {
        int u, v;
        cin >> u >> v;
        add(u, v);
    }

    for( int u = 1; u <= n; u ++ )
        if( !dfn[u] )
            tarjan(u);

    for( int u = 1; u <= n; u ++ )
        for( int i = h[u]; ~i; i = ne[i] )
        {
            int v = e[i];
            if( id[u] != id[v] )
            {//不在同一强联通分量内 统计出度
                dout[ id[u] ] ++ ;
            }
        }

    int zeros = 0, res;
    for( int i = 1; i <= scc_cnt; i ++ )
        if( !dout[i] )
        {
            res = cize[i];
            zeros ++;
            if( zeros > 1 )
            {
                res = 0;
                break;
            }
        }
    cout << res << endl;

    return 0;
}