2022秋招备战！每天写至少一篇Leetcode里Hard难度题目的题解

685. 冗余连接 II

在本问题中，有根树指满足以下条件的 有向 图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi]，用以表示 有向 图中连接顶点 ui 和顶点 vi 的边，其中 ui 是 vi 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

示例 1：

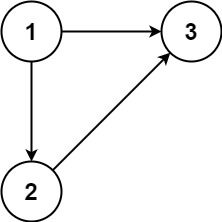
输入：edges = [[1,2],[1,3],[2,3]]
输出：[2,3]

示例 2：

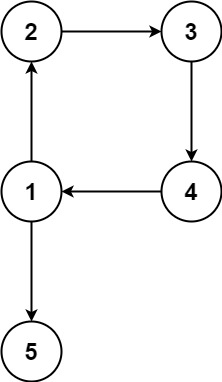
输入：edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出：[4,1]

提示：

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ui, vi <= n

并查集的很有趣的应用。

和684. 冗余连接不一样的是，本题是有向图。因此无法直接判断成环即为树的亢余边。

本题目可以通过样例发现2个情况。

样例1-> 某个点的入度成为了2

样例2->所有的点入度还是一，但是根节点消失了，内部成有向环。

本质上来说，当一颗有向树插入一条额外的边时，是一定会产生一个无向环的。

同时，除非根节点被这条亢余的边连接，否则一定是且只有2个连接某个入度为2的点的边。

因此，我们既要想办法解决这个无向环，又要想办法解决这两个冲突的边。这就是为什么可以用并查集分类讨论的原因。

我们先对所有的点的入度进行讨论，如果有一个点的入度为2（要么有一个要么没有，因为只有一条额外的边）。把这两条边都加入我们的待讨论合集。可以在这里选择倒着保存两条边，或者在和面讨论都可以，因为答案要求我们返回最后一个删除后可能使得树合法的边的答案。

对这个入度为2的点所衍生的两条边进行讨论，用一个并查集来判定失去了这条边的图，是否是一个树即可。

如果没有入度为2的点，则成为了一个有向环，如图二所示。我们从前往后遍历得到第一个成环的边就是我们需要删除的边。原理和684. 冗余连接就一样了。

class UF {
public:
    vector<int> fa;
    vector<int> sz;
    int n;
    int comp_cnt;

public:
    UF(int _n): n(_n), comp_cnt(_n), fa(_n), sz(_n, 1) {
        iota(fa.begin(), fa.end(), 0);
    }

    int findset(int x) {
        return fa[x] == x ? x : fa[x] = findset(fa[x]);
    }

    void unite(int x, int y) {
        x = findset(x);
        y = findset(y);
        if (x != y) {
            if (sz[x] < sz[y]) {
                swap(x, y);
            }
            fa[y] = x;
            sz[x] += sz[y];
            --comp_cnt;
        }
    }

    bool connected(int x, int y) {
        x = findset(x);
        y = findset(y);
        return x == y;
    }
    // 作者：zerotrac2
    // 链接：https://leetcode-cn.com/problems/graph-connectivity-with-threshold/solution/dai-yu-zhi-de-tu-lian-tong-xing-by-zerotrac2/
};
class Solution {
public:
    vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
        int n = edges.size();
        vector<pair<int,int>> v;

        // indegree = 2;
        vector<int> indegree(n + 1, 0);
        for(auto& e: edges) {
            indegree[e[1]]++;
        }
        for (int i = n - 1; i >= 0; i--) {
            if (indegree[edges[i][1]] == 2) {
                v.push_back(pair<int,int>{edges[i][0], edges[i][1]});
            } 
        }
        auto checkTree = [&](int u, int v) {
            UF uf(n + 1);      
            for (auto& e: edges) {
                if (e[0] == u && e[1] == v) continue; // 跳过这条多余的边
                if (uf.connected(e[0], e[1])) return false;
                uf.unite(e[0], e[1]);
            }
            return true;
        };
        if (v.size() == 2) { // 如果有肯定是2个边
            if (checkTree(v[0].first, v[1].second)) return {v[0].first, v[0].second};
            else return {v[1].first, v[1].second};
        }
        // 成环的情况

         UF uf(n + 1);
         for (auto& e: edges) {
             if (uf.connected(e[0], e[1])) return {e[0], e[1]};
             uf.unite(e[0], e[1]);
         }
         return {0,0};
    }
};