AcWing 4207. 最长合法括号子序列    原题链接    中等

作者： 作者的头像   Snowing ,  2022-01-10 10:10:37 ,  所有人可见 ,  阅读 336

1


最长合法括号子序列

题目描述

一个合法的括号序列满足以下条件：

  1. 序列()被认为是合法的。
  2. 如果序列X与Y是合法的，则XY也被认为是合法的。
  3. 如果序列X是合法的，则(X)也是合法的。

例如，()，()()，(())这些都是合法的。

现在，给定一个由 ( 和 ) 组成的字符串。

请你求出其中的最长合法括号子序列的长度。

注意，子序列不一定连续。

输入格式

共一行，一个由 ( 和 ) 组成的字符串。

输出格式

一个整数，表示最长合法括号子序列的长度。

数据范围

前五个测试点满足， 1≤输入字符串的长度≤101≤输入字符串的长度≤10。
所有测试点满足，1≤输入字符串的长度≤1061≤输入字符串的长度≤106。

输入样例1：

(()))(

输出样例1：

4

输入样例2：

()()(()(((

输出样例2：

6

思路分析

image-20220110093337167.png

一个括号序列是合法的括号序列，等价于（结论）

  • 左右括号数量相等（扫描完）
  • 所有前缀中，左括号数量 >= 右括号数量（枚举过程中）

只要上面两个性质成立，就构成合法的括号序列

所以我们在遍历的过程中，只需要维护一个变量cnt，

  • 当遇到左括号的时候，cnt++
  • 当遇到右括号的时候，cnt--

上面两个条件则等价为cnt == 0 和cnt >= 0

接下来，我们分析如何得到最长的括号序列，序列最长，等价于右括号的数量最多，所以，我们采用贪心的思路，每当碰到右括号的时候，能选则选（即cnt>0的时候，碰到右括号一定选)。

即：考虑选右括号，对每个右括号可以选或者不选，我们的策略是从左向右对每个右括号采用贪心的思想选取

贪心的证明

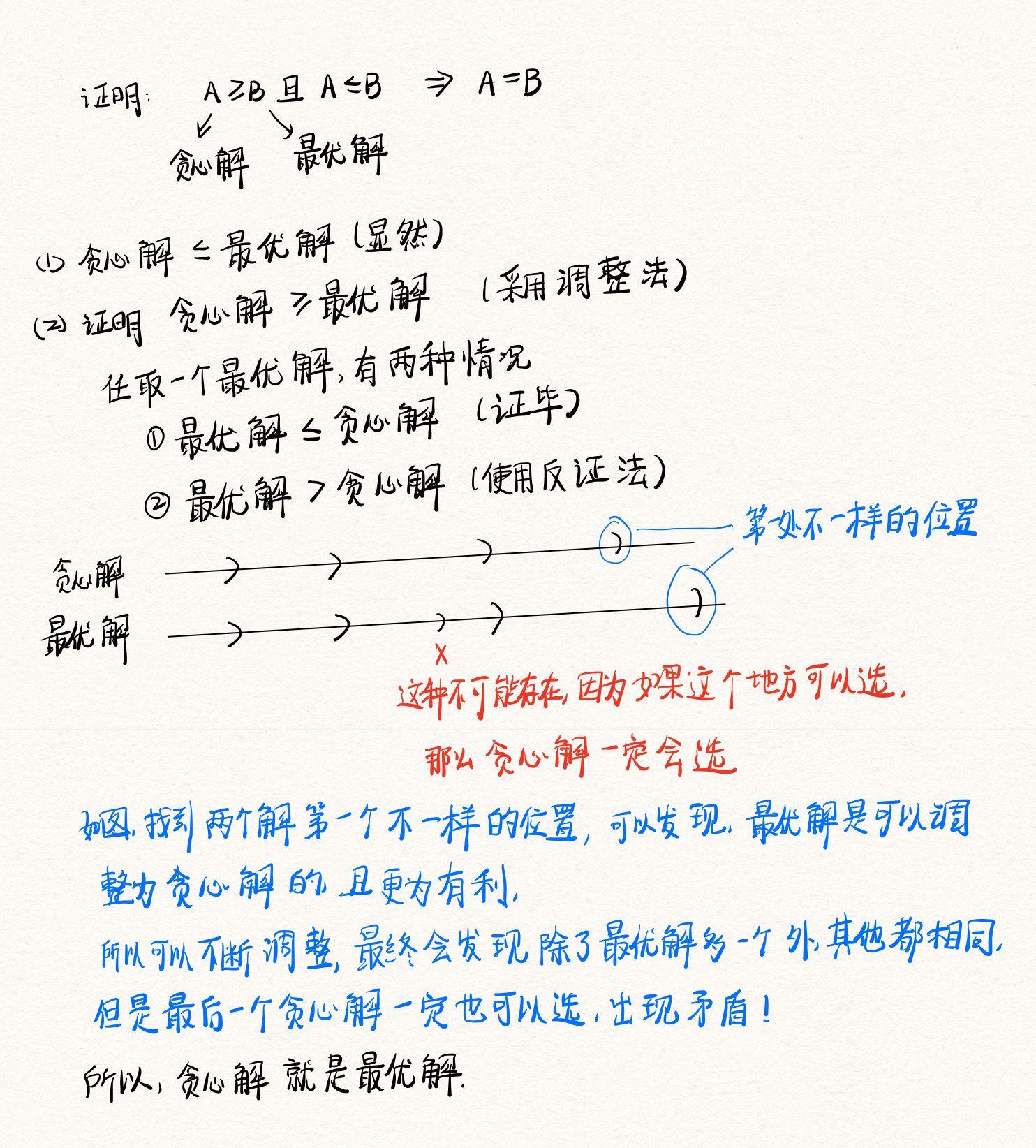
image-20220109153251759.png

代码实现

#include<iostream>

using namespace std;

int main()
{
    string str;
    cin >> str;

    //cnt是题解中用来维护合法括号序列的变量
    //r用来记录一共有多少右括号被加入合法括号序列
    int cnt = 0, r = 0;
    for(auto c : str)
    {
        if(c == '(') cnt++;
        else if(cnt > 0)
        {
            cnt--;
            r++;
        }
    }
    cout << r * 2 << endl;
    return 0;
}

总结

其实这道题目的本质就是使用变量cnt维护已经遍历过的字符串，记录着能够与右括号匹配的左括号数量，cnt>0代表着还能接受右括号，选择右括号的策略是贪心，能选就选。

为什么是右括号，原因在于我们从左向右遍历，右括号进来之后不会对它的右边（之后的遍历）产生影响，而它正好消耗左括号

另一种更加直观的想法，使用一个栈来维护遍历过的左括号

#include <iostream>
#include <stack>
using namespace std;

string str;
stack<char> stk;

int main() {

    cin >> str;

    int r = 0;
    //栈stk中存放的是待处理的左括号
    for (auto c : str) {
        if (c == '(') stk.push(c);//入栈等价于cnt++
        else 
        {
            if(stk.size() > 0) //等价于cnt > 0
            {
                stk.pop();//等价于cnt--
                r++;
            }   
        }
    }

    cout << r * 2;
    return 0;
}

0 评论