优化的dijsktra题解

1.1 建图的节点

• 因为电路是斜向联通的，所以我们所建图中的结点就是所有的格点，如图编号：
  
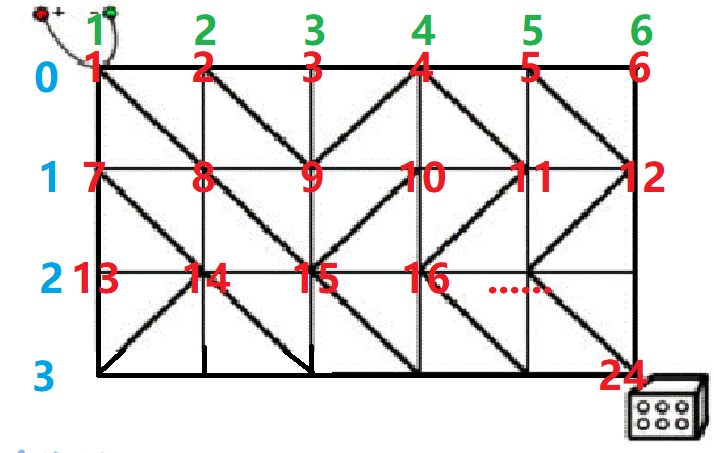
• 红色标记代表编号，蓝号是行号，绿色代表列号
  * 任务：求1好点到(r+1)(c+1)好点的距离

1.2 建边

• 1.2.1
  因为电路是斜向联通的，所以我们所建图中的边就是所有斜向联通的电路及其旋转后的电路
• 1.2.2 样例解释
  黑色电路是样例中给出的，所以使用它不需要任何花费，它也就成为了连接1号点和8号点的边权为0的无向边而灰色电路是黑色电路旋转后得来的，它同样可以被使用，但前提是花费一次操作来进行旋转，所以它就成为了连接 22 号点和 77 号点的边权为 11 的无向边
  同理处理完所有的边，就可以跑最短路啦

1.3 无解情况解释

• 1.3.1
  
  看图一目了然

算法1

C++ 代码

#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int NO_SOLUTION=1061109567;
const int R=504;
const int N=R*R;
const int M=N<<2;
int h[N],r,c,cnt,dis[N];
bool vis[N];
struct edge
{
    int v;
    char w;
    int next;
}e[M];
inline void init()
{
    memset(h,0,sizeof h);
    memset(vis,false,sizeof vis);
    memset(dis,0x3f,sizeof dis);
    cnt=0;
}
inline int dijkstra() // 标准堆优化dijkstra  
{
    priority_queue<pair<int,int> > heap;
    heap.push(make_pair(0,1)); // first = 距离 , second = 结点编号 
    dis[1]=0;
    while(!heap.empty())
    {
        int u=heap.top().second;
        heap.pop();
        if(vis[u]) continue;
        vis[u]=true;
        for(int i=h[u];i;i=e[i].next)
        {
            int v=e[i].v;
            int cost=e[i].w;
            if(!vis[v] && dis[v]>dis[u]+cost)
            {
                dis[v]=dis[u]+cost;
                heap.push(make_pair(-dis[v],v)); // 大根堆通过去相反数变成小根堆 
            }
        }
    }
    return dis[(r+1)*(c+1)]; // 返回到结点 (r+1)*(c+1) 的距离 
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&r,&c);
        init();// 初始化 
        for(int i=1;i<=r;i++)//注意，这里行是从1开始枚举的，所以下文体现为(i-1)
        {
            for(int j=1;j<=c;j++)
            {
                // ===== 获取两边结点编号  =====
                int u1=(i-1)*(c+1)+j;
                int v1=i*(c+1)+j+1;
                int u2=(i-1)*(c+1)+j+1;
                int v2=i*(c+1)+j;

                // ===== 读取电路 ===== 
                char way=getchar();
                while(way!='\\' && way!='/') way=getchar();

                // ===== 加边 ===== 
                e[++cnt]=(edge){v1,way=='/',h[u1]}; h[u1]=cnt;
                e[++cnt]=(edge){u1,way=='/',h[v1]}; h[v1]=cnt;
                e[++cnt]=(edge){v2,way=='\\',h[u2]}; h[u2]=cnt;
                e[++cnt]=(edge){u2,way=='\\',h[v2]}; h[v2]=cnt;
            }
        }
        int ans=dijkstra(); // 跑最短路 

        if(ans==NO_SOLUTION) puts("NO SOLUTION"); // 别忘了判无解 
        else printf("%d\n",ans);
    }
    return 0;
}

拓展算法 SPFA+SLF+LLL 优化

c++代码

#include<cstdio>
#include<cstring>
using namespace std;
const int N=3e5+10;
const int M=3e6+10;
int fi[N],di[M],da[M],ne[M],dis[N],nxt[M],nmb[M],n,m,l;
bool v[N];
//fi,di,da,ne为存边数值,dis记录距离,v记录点有无经过
//nxt,nmb则为数组模拟链表
//nxt记录下一个空间(即后驱)，nmb则为这个空间对应的数据
//因为要实现从队首入队的话自然使用链表是不错的
//而我嫌STL常数过大，所以是用数组来模拟链表
inline int re()//快读
{
    int x=0;
    char c=getchar();
    for(;c<'0'||c>'9';c=getchar());
    for(;c>='0'&&c<='9';c=getchar())
        x=x*10+(c-'0');
    return x;
}
inline int re_l()//读取方格数据并判断是'/'还是'\'的函数
{
    char c=getchar();
    for(;c!='\\'&&c!='/';c=getchar());
    return c=='/'?1:0;
}
inline void add(int x,int y,int z)//加边
{
    di[++l]=y;
    da[l]=z;
    ne[l]=fi[x];
    fi[x]=l;
    di[++l]=x;
    da[l]=z;
    ne[l]=fi[y];
    fi[y]=l;
}
inline int ch(int x,int y)//给每个点一个标签
{
    return (x-1)*(m+1)+y;
}
int main()
{
    int i,j,x,y,t,head,tail,s,ed;
    bool p=1;
    t=re();
    while(t--)//多组数据
    {
        n=re();
        m=re();
        head=l=0;//初始化&清空数组
        s=tail=1;
        p=1;
        ed=ch(n+1,m+1);
        memset(fi,0,sizeof(fi));
        memset(v,0,sizeof(v));
        memset(dis,50,sizeof(dis));
        memset(nxt,0,sizeof(nxt));
        memset(nmb,0,sizeof(nmb));
        for(i=1;i<=n;i++)
            for(j=1;j<=m;j++)//输入方格数据
            {
                if(re_l())//加边方法即为前面所述
                {
                    add(ch(i,j),ch(i+1,j+1),1);
                    add(ch(i+1,j),ch(i,j+1),0);
                }
                else
                {
                    add(ch(i,j),ch(i+1,j+1),0);
                    add(ch(i+1,j),ch(i,j+1),1);
                }
            }
        dis[1]=0;//初始化
        v[1]=1;
        nxt[0]=1;
        nmb[1]=1;
        while(p)//p用来记录有无到达终点，有则直接退出
        {
            head=nxt[head];//每次通过后驱到下一个空间
            if(!head)//若没有后驱了就表明搜索完毕
                break;
            x=nmb[head];//取出该空间对应的数
            for(i=fi[x];i&&p;i=ne[i])//枚举边
            {
                y=di[i];
                if(!v[y]||dis[y]>dis[x]+da[i])//如果没有遍历过或是之前遍历的并不是最短的
                {
                    s++;//给链表申请一个新空间
                    if(da[i])//判断边权
                    {//若为1则从队尾入队
                        nxt[tail]=s;//在链表末端空间打上后驱
                        tail=s;//更新末端
                    }
                    else//若为0则从队首入队
                    {
                        nxt[s]=nxt[head];
                        //将目前遍历的空间的后驱过继给新增空间
                        //即将原本队列置于新增空间后面
                        nxt[head]=s;
                        //将目前遍历的空间的后驱改为新增空间
                        //这样下一次循环就能先遍历新增空间了
                        //于是就实现了将新增空间置于队首的功能
                        if(!nxt[s])
                            tail=s;
                        //一个小细节
                        //若目前队列为空，即队首就是队尾的情况
                        //也要更新末端
                    }
                    nmb[s]=y;//给新增空间附上数值
                    v[y]=1;//记录该点
                    dis[y]=dis[x]+da[i];//修改距离
                    if(y==ed)//若到达终点，直接退出搜索
                        p=0;
                }
            }
        }
        if(p)//若没有到达终点说明无解
            printf("NO SOLUTION\n");
        else
            printf("%d\n",dis[ed]);
    }
    return 0;
}

双端队列+广度优先遍历

• 建边，不转就能联通的建0，需要转才能联通的建1在一张边权只有0/1的图上，可以用双端队列bfs,0边从队头入队，1边从队尾入队

想要知道双端队列代码详细解读，推荐看yls的视频

C++ 代码

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
using namespace std;

const int cap = 500010;
int dist[510][510]; char map[510][510]; bool proc[510][510];
pair<int, int> queue[cap * 2]; int r, c, li, ri;
inline bool valid (int x, int y) { return x >= 0 && x <= r && y >= 0 && y <= c; }
inline void que_add (int x, int y, int v)
{
    if (dist[x][y] < 0 || v < dist[x][y])
    {
        dist[x][y] = v;
        if (li == ri || v > dist[queue[li].first][queue[li].second]) queue[ri++] = make_pair(x, y);
        else queue[--li] = make_pair(x, y);
    }
}
int main ()
{
    int kase; for (scanf("%d", &kase); kase; --kase)
    {
        scanf("%d %d", &r, &c);
        if ((r + c) % 2)
        {
            for (int i = 0; i < r; i++) scanf("%s", map[i]);
            printf("NO SOLUTION\n");
        }
        else
        {
            for (int i = 0; i < r; i++) scanf("%s", map[i]);
            li = ri = cap; queue[ri++] = make_pair(0, 0);
            memset(dist, -1, sizeof dist), dist[0][0] = 0;
            memset(proc, false, sizeof proc);
            while (li != ri)
            {
                int cx = queue[li].first, cy = queue[li].second; ++li;
                if (valid(cx - 1, cy - 1))
                {
                    if (map[cx - 1][cy - 1] == '\\') que_add(cx - 1, cy - 1, dist[cx][cy]);
                    else que_add(cx - 1, cy - 1, dist[cx][cy] + 1);
                }
                if (valid(cx - 1, cy + 1))
                {
                    if (map[cx - 1][cy] == '/') que_add(cx - 1, cy + 1, dist[cx][cy]);
                    else que_add(cx - 1, cy + 1, dist[cx][cy] + 1);
                }
                if (valid(cx + 1, cy - 1))
                {
                    if (map[cx][cy - 1] == '/') que_add(cx + 1, cy - 1, dist[cx][cy]);
                    else que_add(cx + 1, cy - 1, dist[cx][cy] + 1);
                }
                if (valid(cx + 1, cy + 1))
                {
                    if (map[cx][cy] == '\\') que_add(cx + 1, cy + 1, dist[cx][cy]);
                    else que_add(cx + 1, cy + 1, dist[cx][cy] + 1);
                }
            }
            printf("%d\n", dist[r][c]);
        }
    }
    return 0;
}