算法提高课汇总

题意理解

先去掉一个树边, 再去掉一个非树边, 使得新的图变为不连通的两部分.

考虑$u\rightarrow v$路径上若不存在非树边(非树边用红色边表示):

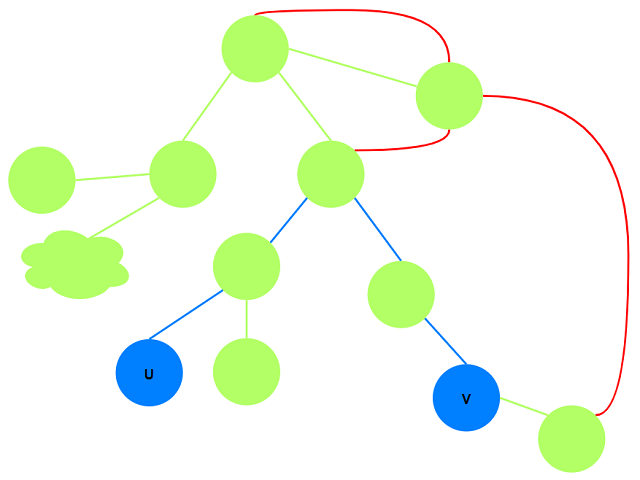
则$u\rightarrow v$路径去掉一条边后, 任意去除一条非树边均满足要求.

考虑$u\rightarrow v$路径上存在一条非树边:

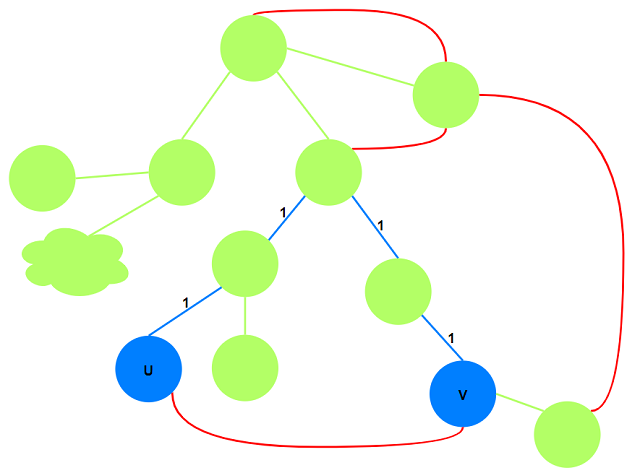
则对于路径中存在一条非树边的边$e$, 若第一次去除$e$, 则第二次去除的非树边必须要是路径上
对应的那个非树边才可满足条件.

考虑路径上存在若干条($\gt 1$)非树边:

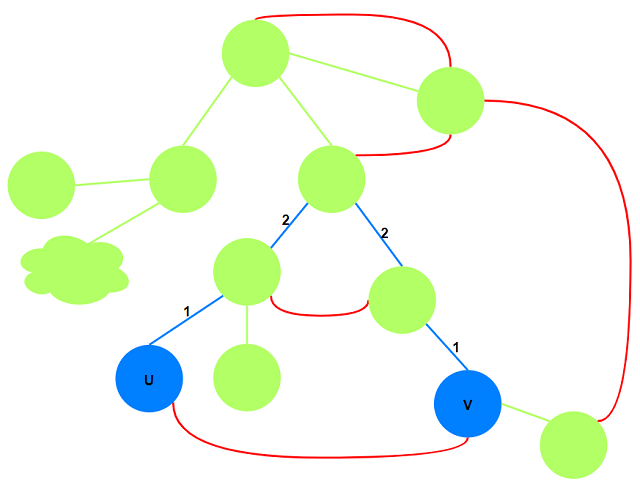
则对于路径中存在大于一条非树边的边$e$, 若第一次去除$e$, 则第二次需要去除大于$1$条对应的
非树边, 无法满足题目要求.

树上差分

此时问题转变为: 对于一条非树边$(u, v)$, 如何快速让$u\rightarrow v$路径上边的计数均$ + 1$.

考虑差分思路: 对于序列差分, 如果某次操作要将区间$[l, r]$上的所有元素值$+c$, 则我们的操作是
$d[l] + c, d[r + 1] - c$, 最后$d[i]$的前缀和即其更新后的值.

用红色表示在前缀和意义上数值增加的区间, 用绿色表示数值减少的区间:

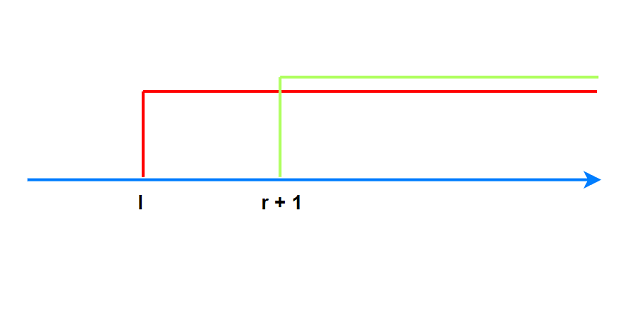
本题采用类似的思路 — 树上差分. 我们知道$u\rightarrow v$的路径可以分为独立的两部分:
$u\rightarrow p$和$v\rightarrow p$, 其中$p$是$u, v$的最近公共祖先. 对非树边$(u, v)$, 我们的操作为
$d[u] + 1, d[v] + 1, d[p] - 2$. 最终前缀和的计算: 以$u$为根子树$d$值的和.

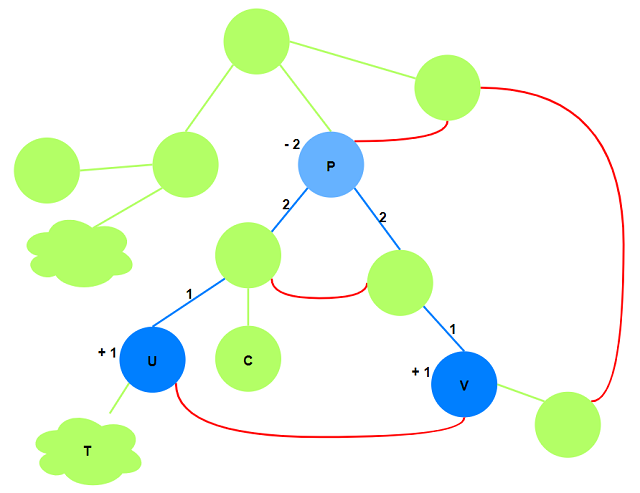
首先考虑操作的正确性:

• 对于$u\rightarrow v$路径上的点(除$p$), 最终计算其作为根的子树中一定包含$u, v$, 所以会被更新.

• 对于$u, v$“之后”或路径的“分支”节点, 如图中的$T$和$C$, 其子树不包含$u$或$v$, 不会被更新.

• 对于$p$以及$p$的祖先节点, 计算$-2+1+1$, 数值上相当于不被更新.

接着思考一个问题: 我们需要更新的是每条边的计数, 此时用节点$d[u]$表示的是那条边的计数?

• 考虑$u\rightarrow v$路径上的节点, $d[p]$与路径无关, 设$u$直接父节点为$pu$, 则每个节点$u$恰好
  与$(u, pu)$一一对应. 具体原理个人暂时无法清楚解释.

具体实现

实现代码 $n\lg(n) + m\lg(n)$

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10, M = 2 * N, lgN = 16;

int n, m;
int h[N], e[M], ne[M], idx;
int depth[N], fa[N][lgN + 1];
int d[N], q[N];
int ans; //记录最终答案

void add(int u, int v)
{
    e[idx] = v, ne[idx] = h[u], h[u] = idx ++;
}

void bfs(int root)
{
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[root] = 1;
    int hh = 0, tt = 0;
    q[tt ++] = root;

    while( hh < tt )
    {
        int u = q[hh ++];
        for( int i = h[u]; ~i; i = ne[i] )
        {
            int v = e[i];
            if( depth[v] > depth[u] + 1 )
            {
                depth[v] = depth[u] + 1;
                q[tt ++] = v;

                fa[v][0] = u;
                for( int k = 1; k <= lgN; k ++ )
                    fa[v][k] = fa[ fa[v][k - 1] ][k - 1];
            }
        }
    }
}

int lca(int u, int v)
{
    if( depth[u] < depth[v] )   swap(u, v);

    for( int k = lgN; k >= 0; k -- )
        if( depth[fa[u][k]] >= depth[v] )
            u = fa[u][k];

    if( u == v )    return u;

    for( int k = lgN; k >= 0; k -- )
        if( fa[u][k] != fa[v][k] )
            u = fa[u][k], v = fa[v][k];
    return fa[u][0];
}

//返回以u为根的d值之和(u到其直接父节点计数的数目)
int dfs(int u, int father)
{
    int res = d[u];
    for( int i = h[u]; ~i; i = ne[i] )
    {
        int v = e[i];
        if( v != father )
        {
            int ret = dfs(v, u);
            if( ret == 0 )  ans += m;
            else if( ret == 1 ) ans += 1;
            res += ret;
        }
    }
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    for( int i = 1; i < n; i ++ )
    {
        int u, v;
        scanf("%d%d", &u, &v);
        add(u, v), add(v, u); 
    }

    bfs(1); //为lca预处理depth[]; fa[][]

    for( int i = 0; i < m; i ++ )
    {//差分
        int u, v;
        scanf("%d%d", &u, &v);
        int p = lca(u, v);
        d[u] += 1, d[v] += 1, d[p] -= 2;
    }

    //计算最终结果
    dfs(1, -1); //root = 1
    printf("%d\n", ans);

    return 0;
}