题目描述

城市的规划在城市建设中是个大问题。

不幸的是，很多城市在开始建设的时候并没有很好的规划，城市规模扩大之后规划不合理的问题就开始显现。

而这座名为 Fractal 的城市设想了这样的一个规划方案，如下图所示：

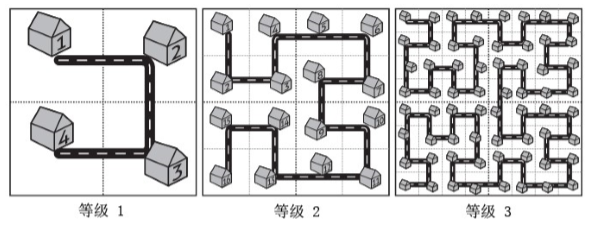
当城区规模扩大之后，Fractal 的解决方案是把和原来城区结构一样的区域按照图中的方式建设在城市周围，提升城市的等级。

对于任意等级的城市，我们把正方形街区从左上角开始按照道路标号。

虽然这个方案很烂，Fractal 规划部门的人员还是想知道，如果城市发展到了等级 N，编号为 A 和 B 的两个街区的直线距离是多少。

街区的距离指的是街区的中心点之间的距离，每个街区都是边长为 10 米的正方形。

数据范围

$1≤N≤31$
$1≤A,B≤22N$
$1≤n≤1000$

样例输入

3 
1 1 2 
2 16 1 
3 4 33 

10 
30 
50 

一开始看视频半天没想明白坐标到底怎么变换的，后来看到一个评论突然就想明白了，这个是按照数组的形式去弄的，$X$向右是增加的，$Y$是向下增加的，左上角是$(0,0)$，之后要注意一下类型，LL len = 1ll << (n - 1), cnt = 1ll << (2 * n - 2);这个移动起来的话$1$是int类型的，会爆掉的，所以要强制转换为long long类型的，用1ll$(是一哎呦哎呦)$。
$z=0$时，左上角，$(x,y)$顺时针旋转$90°$就变成了$(-y,x)$，仔细观察直接顺时针转的话，入口和出口应该对换一下，所以就水平方向翻着，就变成了$(y,x)$。
$z=1$时，右上角，没啥说的直接平移就好了，$(x,y+len)$。
$z=2$时，右下角，也是$(x+len,y+len)$同上。
$z=3$时，左下角，比较难理解的一块，把编号为0的点当做原点$($最初所有编号都进行了$-1$，所以1就变成了$0$，也就是入口$)$，转一下发现还需要进行水平翻转，这时候它就出界了，得向右下方平移，$(2*len-y-1,len-x-1)$，$-1$是因为共用一根边，所以得减去它

#include <bits/stdc++.h>


using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;

PLL calc(int n, LL m) {
    if (n == 0) return {0, 0};
    LL len = 1ll << (n - 1), cnt = 1ll << (2 * n - 2);
    PLL pos = calc(n - 1, m % cnt);
    LL x = pos.first, y = pos.second;
    LL z = m / cnt;
    if (z == 0) return {y, x};
    if (z == 1) return {x, y + len};
    if (z == 2) return {x + len, y + len};
    if (z == 3) return {2 * len - y - 1, len - x - 1};
}

int main() {
#ifdef _DEBUG
    freopen("input.txt", "r", stdin);
//  freopen("output.txt", "w", stdout);
#endif
    int T;
    cin >> T;
    while (T--) {
        LL n, A, B;
        cin >> n >> A >> B;
        PLL ac = calc(n, A - 1);
        PLL bd = calc(n, B - 1);
        double x = ac.first - bd.first;
        double y = ac.second - bd.second;
        printf("%.0lf\n", sqrt(x * x + y * y) * 10);
    }
    return 0;
}